0. reference
https://arxiv.org/abs/1502.03167
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Training Deep Neural Networks is complicated by the fact that the distribution of each layer's inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful param
arxiv.org
1. Introduction
1.1. SGD(Stochastic Gradient Descent)?
- SGD는 Loss Function(손실함수)의 값을 줄이기 위한 방법중 하나이다.
- SGD를 수식으로 나타내면 다음과 같다.(Optimization들은 다 이런 수식이라고 생각하면 된다.)
- 즉, 손실함수가 최소값을 갖도록 하는 신경망의 parameter를 update하는 것과 같다.

1.2. Covariate shift(공변량 변화)
- 이러한 SGD의 문제점은 초기의 parameter 설정에 되게 신중한 조정이 필요하고,
- 각 층을 지날때마다 들어오는 데이터의 분포가 각 층마다 달라지게 되는데, 이를 "Covariate Shift"라고 한다.
- 이를 해결하지 않으면 학습이 어려워 질 수 있다. 즉, 각 층의 분포가 서로 거의 비슷하게 형성되어야 학습이 잘 된다는 것이다.
- 해당 논문에서 hidden layer(은닉층)에 해당하는 Covariate Shift를 "Inner Covariate Shift"라고 정의한다.
1.3. Batch Normalization(배치 정규화)
- Batch Normalization은 Inner Covariate Shift를 줄이기 위해 나오게 된 기법이다.
- Batch Normalization의 장점은 다음과 같다.
"""
i) 학습 가속화
ii) 높은 Learning Rate 사용 가능
iii) Drop-out의 필요성 감소
"""
2. Towards Reducing Internal Covariate Shift
2.1. whitening(화이트닝)
- 신경망의 성능과 학습 속도를 향상시켜주기 위해서 입력이 whitening(화이트닝)되면 좋다고 알려져 있다.
- 여기서 whitening이란, 입력값을 선형변환을 통해 평균이 0, 분산이 1로 되게 맞추어 상관관계를 제거하는 것을 의미한다.
- 즉, 은닉층의 모든 입력값이 whitening시킨다면 더욱 더 좋은 효율을 보여줄 수 있다는 것을 짐작할 수 있다.
- 하지만, 각 레이어의 층마다 whitening을 하게 되면 Backpropagation을 할 때 많은 연산이 필요하게 되서 결과적으로 비효율적이다.
3. Normalization via Mini-Batch Statistics
3.1. Batch Normalizatio(배치정규화) 순전파
- 앞서 2.1에서 화이트닝의 단점을 커버하기 위해서 나온게 Mini-Batch마다 정규화를 해주는 아이디어이다.
- 각 배치마다 d-차원을 가진 input x가 있다고 생각하자

- 이를 각 차원마다 다음과 같은 Normalization을 적용해준다. (이렇게 되면 평균은 0, 분산은 1로 조정된다.)
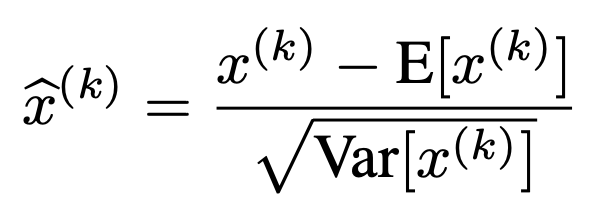
- 하지만 이렇게 Normalization을 한다고 해서 끝나는 것이 아니다.
- 이 상태 그대로 Activation Function중 하나인 Sigmoid함수에 넣게되면,
- 선형함수에 넣게 되는 것과 같은 효과를 보이기에 학습에 적절하지 못하다.

- 그래서 정규화한 값을 scaling 하고 shift하여 sigmoid에서 선형적인 구간을 벗어나도록 해야한다.

- 여기서 감마와 베타는 학습가능한 parameter이다.
3.2. Batch Normalization 순전파 코드 구현
- 해당 알고리즘을 보면서 실제로 구현해보면 다음과 같다.(layer지만 편의상 함수로 간단히 나타내었다.)

def BN(x):
mu = np.mean(x,axis=0)
var = np.var(x,axis=0)
x_hat = (x-mu) / (np.sqrt(var)+0.001)
return x_hat*gamma + betta #gamma,betta: 학습가능한 parameter
3.3. Batch normalization 역전파
- 배치정규화의 gamma, betta를 학습시키기 위해선 역전파를 구해야한다.
- 역전파는 다음과 같이 구할 수 있다.

3.4. Batch Normalization 역전파 코드구현
def backward(dout):
dbeta = dout.sum(axis=0)
dgamma = np.sum(xn * dout, axis=0)
dxn = gamma * dout
dxc = dxn / std
dstd = -np.sum((dxn * xc) / (std * std), axis=0)
dvar = 0.5 * dstd / std
dxc += (2.0 / batch_size) * xc * dvar
dmu = np.sum(dxc, axis=0)
dx = dxc - dmu / batch_size
return dx
3.5. test할때의 Batch Normalization?
- train일때는 분산과 평균을 그때 그때 구할 수 있지만, test일때는 불가능하다.
- 그래서 test일때 Batch Normalization layer에 들어가게 되는 평균과 분산은 다음과 같다.
(train일때의 평균과 분산을 따로 저장해둔다.)

- 이러한 이유는 모집단의 추정을 토대로 나온다는 것을 알 수 있다.
4. conclusion

- 실제로 다음과 같이 BN을 적용했을때가 적용하기 전보다 빠르게 ACC가 올라가는 것을 알 수 있다.
