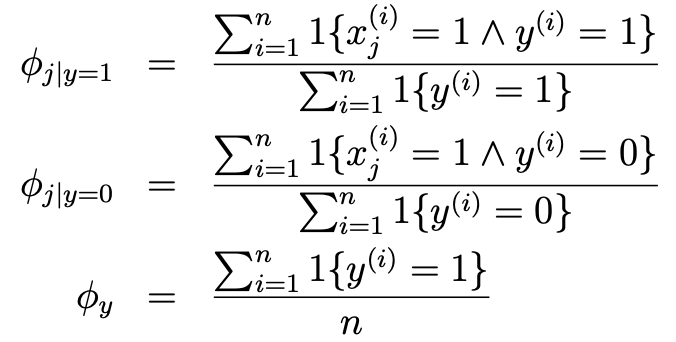[CS229] [5] Lecture 5 - GDA & Naive Bayes

1. Generative learning algorithms

- 본격적으로 시작하기전에 간단하게 binary classification을 봐보자.

- 다음과 같은 데이터가 주어져 있다고 해보자.

 

- 그러면, gradient descent을 이용하거나 Normal equation을 이용하여

- parameters을 update하여 다음과 같은 binary classification을 이룰것이다.

 

 

- 이를 discriminative learning algorithms이라고 하는데,

- P(y|x)을 학습하는것과 같다. (ex, h(x) = {0,1})

 

- 이와 대조되는 건 Generative learning algorithms이라고 한다.

- 즉, P(x | y)을 학습하는 것과 같다. (x : feature , y : class)

- ex) 종양이 양성이라면(y), --> 어떤 특징이 있을까(x)

- 그 후 p(y)를 학습한다.(class priors)

- ex) 마치 환자를 보자마자 양성,음성을 판단하는 확률

 

1.1. Bayes rule

- Bayes rule는 다음과 같이 정리된다.

- 여기서 p(x)는 다음과 같다.

p(x) = p(x | y = 1)p(y=1) +p(x | y = 0)p(y=0)

 

2. Gaussian discriminant Analysis(GDA)

- GDA는 model이 p(x|y)를 assume할 때, multivariate normal distribution에 분포한다고 생각하는 걸의미한다.

- multivariate normal distribution이 무엇인지에 대해서 알아보자.

2.1. The multivariate normal distribution

- 우리는 일변수 정규분포에 대해선 잘 알고있다.

- 여기서 일변수가 아니라 다변수로 일반화한 정규분포라고 생각하면 된다.

- 다음과 같은 pdf을 가진다.

- mu : x의 mean vector이다.

- sigma : covariance matrix

- sigma = Cov(Z) = E[(Z-E[Z])(Z-E[Z])^T]=E[ZZ^T]=(E[Z])(E[Z])^T

- 그래프로 나타내면 다음과 같은 형태를 뛴다. (변수가 2개라고 생각)

 

 

- sigma의 행렬이 어떤 행렬을 가지냐에 따라서 분포의 모양이 달라지게 된다.

 

2.2. The Gaussian discriminant analysis model

- 연속값을 가지는 random variable인 input features x를 분류(이진 분류)하라는 문제가 주어지면,

- 우리는 GDA(Gaussian discriminant analysis)모델을 사용할 수 있다.

- P(x|y)를 multivariate normal distribution으로 모델링한다. 

 

 

- 이를 바탕으로 log-maximum likelihood를 구해보면 다음과 같다.

- 이게 최대가 되려면 Parameter 4개가 다음과 같으면 된다.

- 조금만 생각해보면 바로 알 수 있으니 넘어가자.

- 이를 바탕으로 contour를 그려보면 다음과 같다.

 

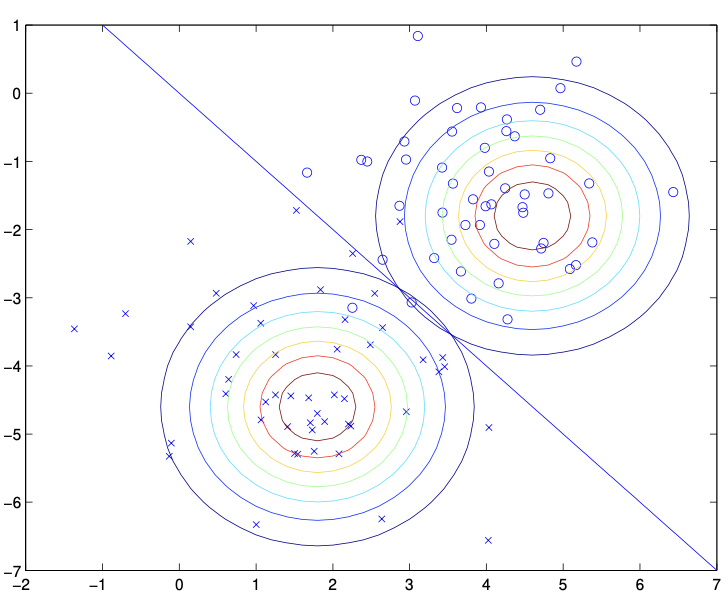
2.3. GDA and logistic regression

- GDA는 Logistic regression과 흥미로운 관계를 가지고 있다.

- p(y=1 | x)을 x의 함수로 본다면, 해당 값은 다음과 같은 형태로 표현이 가능하다.

 

 

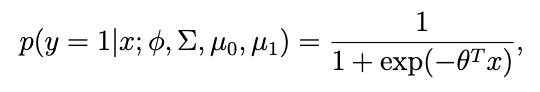
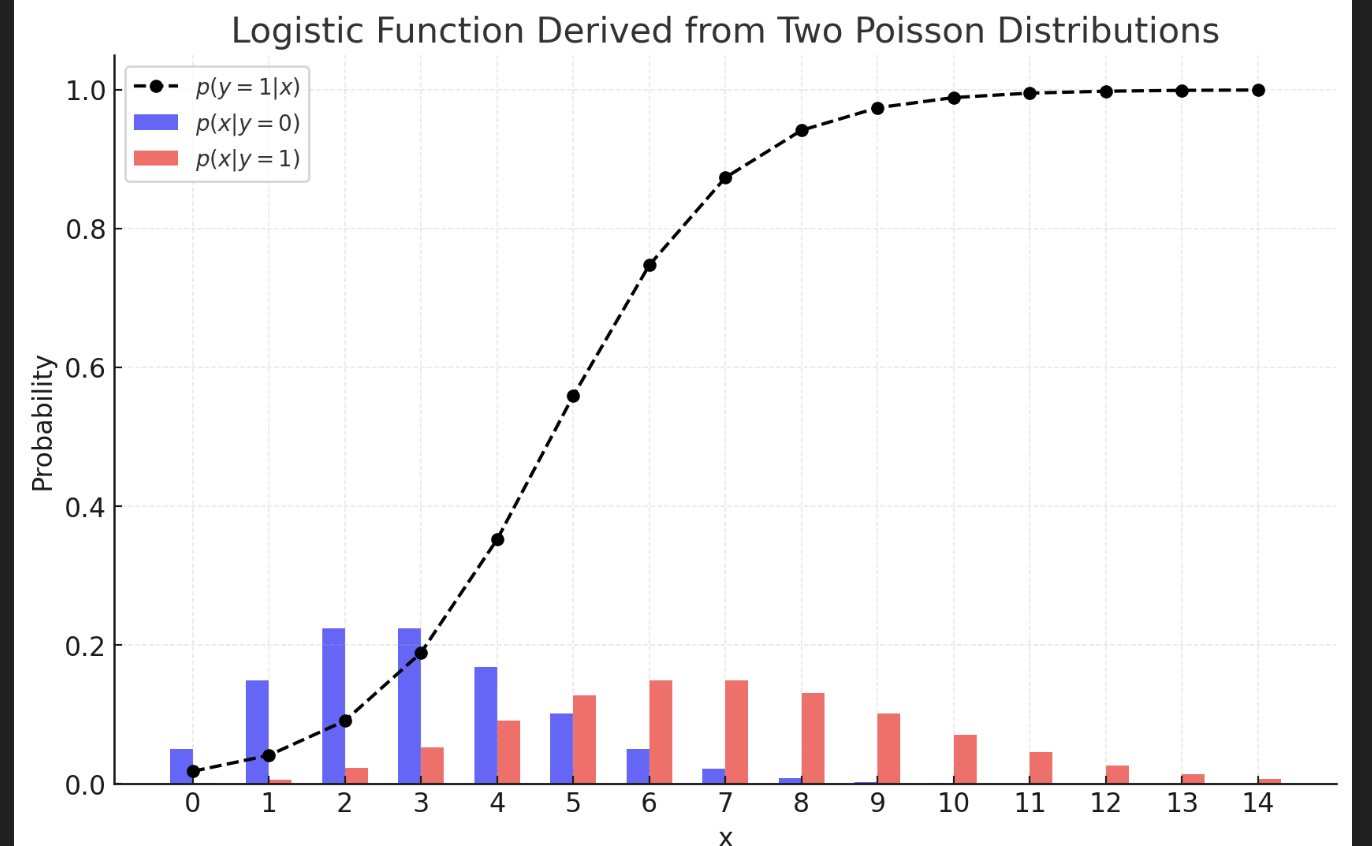
- 정규분포나 푸아송분포더라도 Logistic function이 유도됨을 알 수 있다.

 

2.4. GDA는 Logistic과 비슷하다?

- GDA는 dataset의 분포 즉, hypothesis가 거의 확실하다면 어떠한 모델보다 정확하다고 한다.

- 하지만 그만큼 확실하지 않다면 바로 안좋은 성능을 보인다. 

- data set 이 적다면 GDA가 유리, dataset이 크다면 Logistic regression이 유리하다고 한다.

 

3. Naive bayes

- 우리는 앞서 GDA에선 feature vector x가 연속적이였다.

- 이번엔 이산값을 가질 때의 학습 알고리즘에 대해 알아보자.

- 머신러닝을 이용하여 이메일 스팸 필터를 만든다고 생각해보자.

- 즉, 메시지를 분류하여 스팸인지 스팸이 아닌지 판단하려고 한다.

 

- 스팸 필터를 구성하기 위해 스팸 또는 스팸이 아닌 것으로 라벨이 지정된 이메일로 구성된 train dataset이 있다고 가정하자.

- 이메일을 표현하는 데 사용되는 feature x를 저정하여 스팸 필터를 설계할 것이다.

 

- email을 Dictionary에 있는 단어 수와 동일한 길이의 특지 벡터로 표현할 것이다.

- 예를 들어, 이메일이 사전에서 j번째 단어를 포함하고 있으면 x[j] = 1, 그렇지 않으면 0 으로 설정한다.

- 다음 그림을 보면 이해하기 쉬울것이다.

 

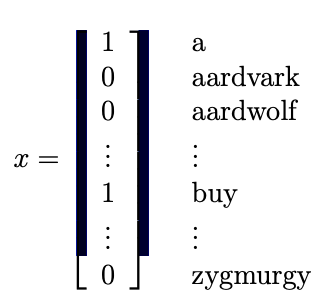
- 이제 generative model을 구축하고자 한다.

- p(x | y)를 모델링해야한다.

- 만약 우리가 50,000개로 이루어진 vocabulary를 가지고 있다면 

 

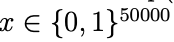
- 이는 마치 2^50000개의 가능한 결과에 대한 multinomial distribution으로 모델링한다고 가정하면,

- 2^50000 -1 차원의 parameter vector을 갖게 된다.

- 이는 너무 많은 parameter를 요구한다.

 

- 이를 해결하고자 p(x|y)를 모델링하기 위해 매우 강한 가정을 세워보자.

- x[i]가 y를 기준으로 전부 독립이라고 가정하자. (이 가정을 Naive Bayes, NB가정)

- 이러한 Naive Bayes를 이용하여 생성된 알고리즘을 Naive Bayes Classifier라고 한다.

 

- 예를 들어, y = 1이 스팸 이메일을 의미한다고 해보자.

- "buy"를 2087번쨰 단어, "price"를 39831번째 단어라고 가정해보자.

- NB가정이라면 다음과 같은 결과가 나온다.

P(x[2087] | y) = p(x[2087] | y ,x[39831])

 

 

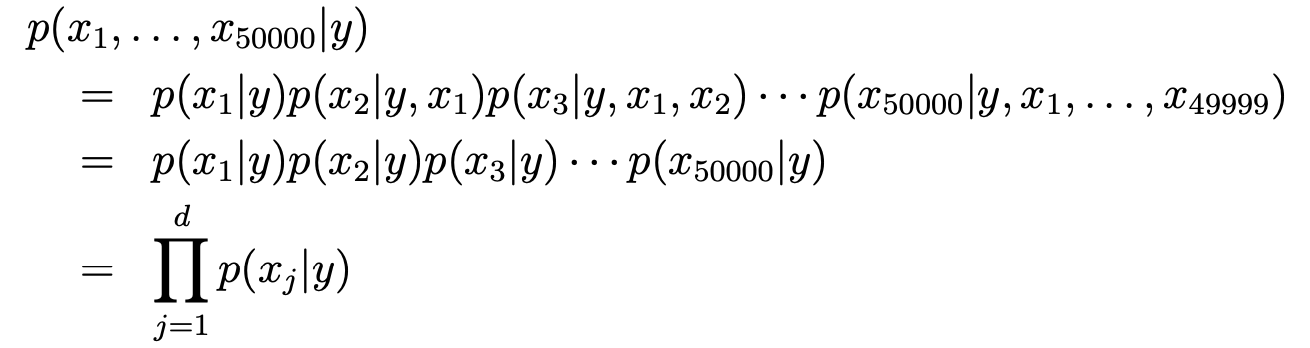
- 이러한 사실을 바탕으로 joint likelihood를 나타내면 다음과 같아진다.

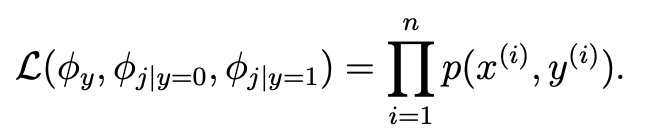
- MLE를 만족하는 파라미터들을 구해보면 다음과 같다.