[논문 리뷰] [NLP] End-To-End Memory Networks

0. Reference

https://arxiv.org/abs/1503.08895

End-To-End Memory Networks

1. Introduction

- 현재 연구에서 포커싱하고 있는 도전 과제는 두 가지이다.

- 첫 번째 : QA 문제를 해결하기위해 여러 계산 단계를 수행할 수 있는 모델을 구축하는 것(Backpropagation)

- 두 번째 : Sequence 데이터에서 long-term dependencies을 잘 학습할 수 있는가

- 이러한 두가지 도전 과제를 해결하기 위한 End-to-End momory networks을 본 논문에서 설명한다고 한다. 

 

2. Approach

- 해당 모델은 메모리에 저장될 "discrete input set x1,...,xn", "query q", "answer a"를 처리한다.

- 여기서 xi, q,a는 사전에 포함된 V개의 단어 중 일부를 포함하는 기호(symbol)으로 구성된다.

- 모델은 모든 xi를 고정된 버퍼 크기까지 메모리에 저장한 뒤, x와 q에 대한 Continuous한 representation을 찾게 된다.

- Continuous representation을 multiple hops을 통해 출력 a를 생성하게 된다.

- 여기서 Hop이란, 출력 symbol하나를 생성하는 동안 여러 계산 단계를 수행하는 방식을 의미한다.

 

- 이러한 과정이 학습 중 error signal이 메모리를 거쳐 backpropagation될 수 있도록 도움을 준다고 한다.

 

2.1. Single Layer

- single layer에서는 한개의 hop으로 이루어져 있는데, 이러한 single layer가 쌓이면 multiple hops를 구현하게 된다고 한다.

2.1.1. Input Memory Repesentation

- input data x1,...xi가 메모리에 저장된다고 가정해보자.

- 전체 input set {xi}는 memory vectors {mi}로 변환되며, 이 벡터들은 d차원을 갖게 된다고 해보자.

- 이 때의 과정은 간단하게 embedding matrix A를 사용하여 Affine 하는 과정이라고  생각하면 된다.

 

- query q도 마찬가지로 Embedding matrix B(A와 동일 차원)를 사용하여 {u}를 계산하게 된다.

- 그 후, 벡터 u와 mi 사이의 inner product를 계산하고, 이를 Softmax를 적용하여 일치하는 정도를 probability vector를 계산한다.

 

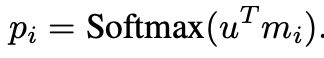
2.1.2. Output Memory Representation

- 위 과정과 마찬가지로, 각 입력 xi에는 output vector ci가 mapping되게 되는데,

- 이 벡터는 또다른 embedding matrix C를 사용하여 생성된다.

- 최종적으로 output memory response vector o 는 다음과 같이 계산된다.

 

2.1.3. Generating the Final Prediction

- songle later에서는 output vector o와 input embedding u의 합을 weight matrix W를 통과하고,

- Softmax를 적용하여 Predict Label을 생성하게 된다.

 

2.2. Multiple Layers

- 이제 Single layer에서 Multiple Layers로 확장해보자.

-이를 위해, memory layers을 여러 개를 쌓는 방식을 사용하게 된다.

- 우선, 각 layer의 입력은 이전 layer의 출력 o와 입력 u의 합으로 정의된다.

 

- 각각의 Embedding vector를 계산하기 위해 각 Layer에서는 서로 다른 Embedding Matrix A,C를 사용하게 되는데,

- 이는 아주 많은 계산 비용이 들기에, 이에 제약을 걸어줄 필요가 있다.

- 본 논문에선 해당 제약 두가지를 설명한다.

i) Adjacent 방식

- 한 layer의 output embedding Matrix를 다음 계측의 input Embedding matrix로 사용하는 것이다.

- 추가적으로 다음과 같은 제약도 적용하였다고 한다.

 

ii) Layer-wise 방식 (RNN과 유사)

- 모든 layer에서 동일한 입력 및 출력 embedding Matrix를 공유하는 것이다.

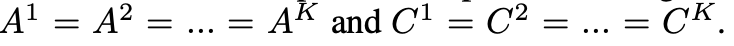
- 이 때, Affine matrix H를 추가하여 hop간의 업데이트를 수행한다고 한다.