[R4DS] [3-1] 탐색적 데이터 분석(EDA)
1. EDA?
- 해당 챕터에서는 데이터를 체계적으로 탐색하기 위해 시각화 및 탐색을 활용하는 과정을 정리할 것이다.
- 해당 작업을 탐색적 데이터 분석 또는 EDA(Exploratory Data Analysis)라고 한다.
- 다음과 같은 반복적인 작업으로 이루어져 있다.
1. 데이터에 대한 질문 만들기.
2. 데이터를 시각화,변형 및 모델링하여 질문에 대한 답 찾기.
3. 질문을 개선하거나 새로운 질문을 만들기 위해 학습한 방법을 사용
-EDA는 엄격한 규칙을 가진 형식적인 과정이 아닌 사고하는 상태 그자체이다.
-EDA는 모든 데이터 분석에서 중요한 부분을 차지
--> 그이유는 질문이 주어진다고 해도 데이터의 품질은 항상 조사해야하기 때문이다.
-데이터 정제를 하기 위해서는 EDA의 모든 도구(시각화, 변형 및 모델링)을 사용해야함
2. 질문하기
- EDA의 목표는 데이터를 이해하는 것이다.
- 가장 쉬운 방법은 탐색을 위한 도구로 질문을 사용하는 것이다.
- 데이터 셋의 특정부분에 집중하며 어떤 그래프, 어떤 모델을 만들지 또는 어떻게 변형을 할지 결정하는 데 도움을 준다.
-EDA는 근본적으로 창의적인 과정이다.
- 그래서 좋은 질문을 하는 핵심은 많은 양의 질문을 생성하는 것이다.
- 각각의 새로운 질문들은 자신을 데이터의 새로운 측면에 노출시키고 발견할 기회를 증가시킨다.
- 탐색을 위해 어떤 질문을 해야 하는가에 대한 규칙은 없다.
- 하지만, 데이터에서 발굴할 수 있는 언제나 유용한 두 가지 유형의 질문이 있다.
Q1) 변수 내에서 어떤 유형의 변동이 발생하는가?
Q2) 변수 간에 어떤 유형의 공변동이 발생하는가?
- 이번 챕터에선 변동과,공변동에 대해서 알아가게 될것이고 각 질문에 대한 몇 가지 답변을 제시받을 것이다.
-용어 정의
a) 변수(variavle)
- 측정할 수 있는 양
b) 값(value)
- 변수가 측정될 때의 상태
c) 관측값(observation)
- 유사한 조건에서 측정된 값들의 집합
--> 관측값을 데이터 포인트 라고 부르기도 한다.
3. 변동
- 변동(variation)은 변수의 측정값이 변하는 경향을 말함
- 모든 변수는 흥미로운 정보를 나타낼 수 있는 고유한 변동 패턴을 가지고 있음
- 이러한 패턴을 이해하는 가장 좋은 방법은 변수들 값의 분포를 시각화하는것
4. 분포 시각화
- 변수의 분포를 시각화 하는 방법은 그 변수가 범주형인지 연속형인지에 따라 달라진다.
a) 범주형(categorical)
- 유한개의 집합에서 하나의 값만 가질 수 있는 경우
- R에서 범주형 변수는 일반적으로 팩터형이나 문자형 벡터로 저장됨
- 범주형 변수의 분포를 확인하기 위해서는 막대그래프를 사용
ex)
ggplot(data = diamonds) +
geom_bar(mapping = aes(x = cut, fill = cut))
- 막대의 높이는 각 x값에 대한 관측값의 수를 나타낸다.
b) 연속형(continuous)
- 순서가 있는 무한 집합에서 임의의 값을 가질 수 있는 변수
- 연속형 분포를 확인하기 위해서는 히스토그램을 사용한다.
ex)
ggplot(data = diamonds) +
geom_histogram(mapping = aes(x = carat), birwidth = 0.5)
smaller <- diamonds %>%
filter(carat <=3)ggplot(data = smaller, mapping = aes(x = carat)) +
geom_histogram(binwidth = 0.1)
ggplot(data = smaller, mapping = aes(x = carat, color = cut)) +
geom_freqpoly(binwidth = 0.1)
5. 일반적인 값
- 막대그래프와 히스토그램 모두 길이가 긴 막대는 빈도가 높은 값을 나타냄
- 짧은 막대는 빈도가 낮은 값을 나타냄
- 막대가 생기지 않은 부분은 해당 값의 데이터가 존재하지 않다는 것을 의미
6.이상값
- 이상값은 패턴과 맞지 않는 데이터 값으로 비정상적인 관측값의미
- 이상값은 데이터 입력 오류 or 중요하면서 새로운 정보를 제시
- 많은 양의 데이터가 있을 때 히스토그램에서 이상값을 발견하는 것은 어려움
ex) 다이아몬드 데이터셋에서 y변수의 분포를 그리는 경우, 이상값의 유일한 단서는 x축의 범위가 넓다는 것
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5 )
- 다음과 같이 이상하게 값이 없지만 x축이 너무 길게 나와있음을 알수 있다.
- 일부 빈의 길이가 너무 짧아 눈으로 확인하기 어렵기 때문에 육안으로 보기 힘들다.
- 이를 해결하기 위해선 coord_cartesian()을 사용하여 y축의 작은 값들을 확대해야 한다.
- coord_cartesian() :
- x축과 y축의 범위를 설정하여 그래프에서 보여지는 데이터의 영역을 조절할수있다.
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5 ) +
coord_cartesian(ylim = c(0,50))
7. 연습문제
Q1) diamonds의 x,y 및 z 변수의 분포를 탐색해보자. 어떤 것을 알게 되는가? 다이아몬드에 대해 생각해보고 어떤 치수가 길이,너비,깊이인지 결정해보자.
- x : 'red' , y = 'green', z = 'purple'
ggplot(diamonds) +
geom_freqpoly(mapping = aes(x), binwidth = 0.1,color = 'red') +
geom_freqpoly(mapping = aes(y),binwidth = 0.1 ,color = 'green') +
geom_freqpoly(mapping = aes(z),binwidth = 0.1, color = 'purple') +
coord_cartesian(xlim = c(0,10))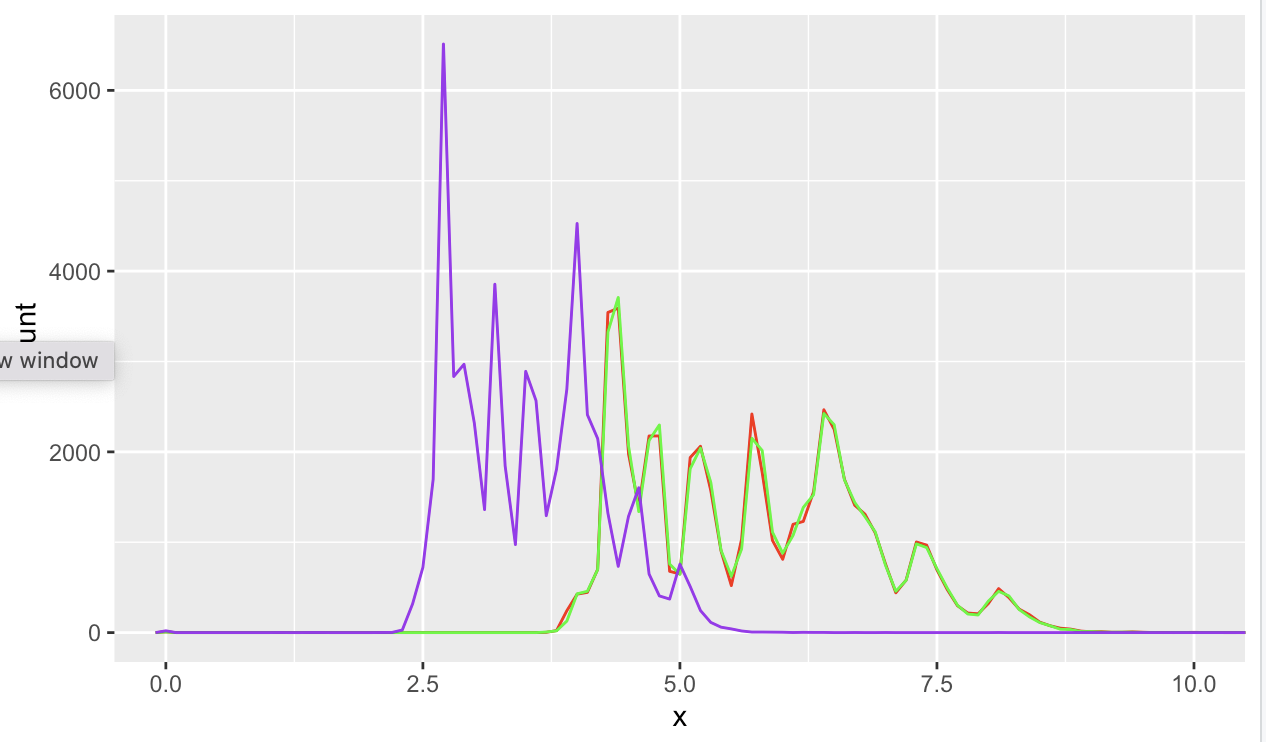
-x,y 의 분포는 거의 동일하고 , z는 상대적으로 앞에 위치한다.
- x : 길이, y : 너비, z : 높이
Q2) price의 분포를 탐색해보자. 뭐가 특이하거나 놀랄 만한 것이 보이는가?
ggplot(diamonds) +
geom_histogram(mapping = aes(x=price), binwidth = 10,fill = 'lightgreen')
-전체적으로 반비례하는 관계로 보이는데 놀라운 점은 price가 끊겨있다라는 점이다.
Q3) 0.99캐럿인 다이아몬드는 몇 개이고, 1캐럿은 몇 개인가?
r <- select(diamonds,carat) %>%
filter(carat == 0.99)> nrow(r)
[1] 23 r <- select(diamonds,carat) %>%
filter(carat == 1.00)nrow(r)
[1] 1558
