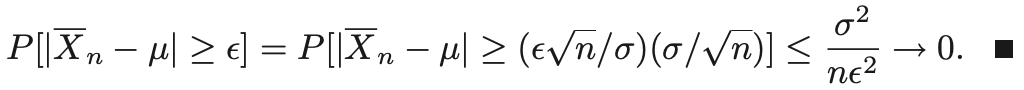[수리통계학] [5.1] Convergence in Probability

1. Introduction

1.1. Difinition [1] : Convergence in Probability

- {Xn}을 R.V의 sequence라고 하고, X를 어떤 표본 공간에서 정의된 R.V라고 하자.

- 만약 모든 epsilon >0 에 대해

- 이를 만조하면, Xn이 X에 Convergence in probability한다고 한다.

- 이를 다음과 같이 표기한다.

 

1.2. Theorem [1] : Weak Law of Large Numbers(WLLN)

- iid를 따르는 R.V의 sequence {Xn}이 평균 mu와 분산 sigma^2을 갖는다고 하자.

- 표본 평균을 다음과 같이 정의하자.

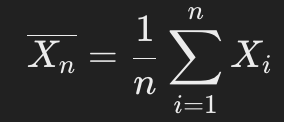
- 그러면 다음을 만족한다.

 

- 증명은 간단히, 쳬비세프 부등식을 적용하여 증명 가능하다.