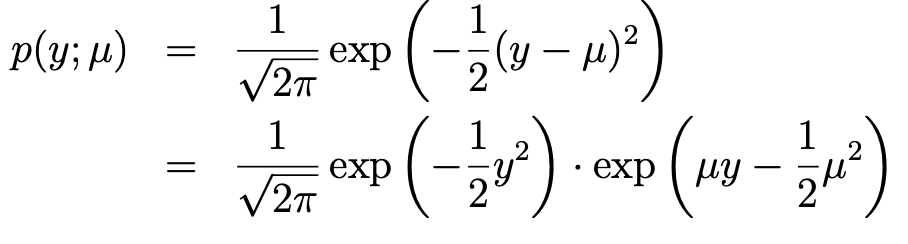[수리통계학] [7.5] The Exponential Class of Distributions

1. The exponential family

- The exponential family는 다음과 같은 PDF을 만족하는 분포를 의미한다.

 

- b(y) : base measure

- y : data

- eta : natural parameter

- T(y) : sufficient statistic(여기선 y와 같은 값을 가진다고 생각해도 무관)

- a(eta) : log partition function

1.1. Bernoulli distribution

- 베르누이 분포를 다음과 같이 식정리를 해보자.

- 그러면 the exponential family에 속한다는 것을 알 수 있다.

- 여기서 eta에 집중해보자, eta를 phi에 대해서 정리하면 다음과 같은 형태가 나오게 된다.

phi = 1 / (1 + e^-eta) 마치 sigmoid function과 유사한 형태가 나오게 된다. (이는 나중에 더 자세히 알아보자.)

 

1.2. Gaussian distribution

- 이번엔 분산이 1인 정규분포를 생각해보자.(분산이 1인이유는 간단하게 보기 위함)

- 그러면 다음과 같이 the exponential family에 속한다는 것을 알 수 있다.

1.3. 왜 the exponential family에 대해 알아야 할까?

- the exponential family에 속하면 다음과 같은 특징이 있다.

- 가장 큰 특징은 이것이다.

- Exponential Family에 속하는 분포에대해 Maximam likelihood를 진행하게 되면, optimize problem을 concave하게 풀 수 있게된다.