[R4DS] [3-3] 공변동
1.공변동(covariation)
- 둘 이상의 변숫값이 연관되어 동시에 변하는 경향을 말함
- 공변동을 발견하는 가장 좋은 방법 : "두 개 이상의 변수 사이의 관계를 시각화 하는 것"
2. 범주형 변수와 연속형 변수
- 이전의 빈도 다각형(히스토그램)과 같이 범주형 변수로 구분된 연속형 변수의 분포를 탐색하고자 하는 것이 일반적이다.
-geom_freqploy()의 기본 모양은 뫂이가 빈도수를 나타내기 때문에 그러한 종류의 비교는 유용X
--> 즉, 그룹 중 하나가 다른 값들보다 월등히 작으면 형태의 차이를 파악하기 어려움
ex) 다이아몬드의 가격이 품질에 따라 어떻게 달라지는지 확인해보자.
ggplot(data = diamonds, mapping = aes(x = price)) +
geom_freqpoly(mapping = aes(color = cut), binwidth = 500)
- 전체적인 빈도수가 많이 다르므로 분포의 차이를 파악하기 어렵다.
ggplot(data = diamonds) +
geom_bar(mapping = aes(x = cut))
- 비교를 쉽게하기 위해 y축에 표시된 빈도수를 빈도수를 표준화한 밀도로 나타내보자.
ggplot(
data = diamonds,
mapping = aes(x = price , y = ..density..)
) +
geom_freqpoly(mapping = aes(color = cut), binwidth = 500)
- 해당 플롯에는 놀라운 점을 확인할 수 있다.
- fair인 다이아몬드가 가장 높은 평균 가격을 가진다는 것이다.
- 이 이유는 이 빈도 다각형에는 작업해야 하는 부분이 남아있기 때문에 당장 해석하기 어렵기 때문이다.
2.1 BOX PLOT
- 범주형 변수로 구분된 연속형 변수의 분포를 나타내는 또 다른 방법은 boxplot이다.
- 박스 플롯은 값의 분포를 시각적으로 간편하게 보여줄 수 있는 형태 ==> 많은 통계학자가 사용하는 방법이다.
- BOXPLOT은 다음의 것들로 구성됨
i) IQR(사분위수범위) : Q3(75번째 백분위수) , Q2(50번째 백분위수), Q1(25번째 백분위수)
--> IQR = Q3-Q1
ii) 상자의 가장자리에서 1.5*IQR 이상 떨어진 관측값을 나타내는 점
iii) 상자의 양끝에서 뻗어 나와 가장 멀리 떨어진 이상값이 아닌 점까지 이어진 선
iv) 이상값

- geom_boxplot()을 사용하여 컷팅에 따른 가격의 분포를 살펴보자
ggplot(data = diamonds, mapping = aes(x=cut,y = price)) +
geom_boxplot()
- 박스 플롯은 분포에 대해 더 적은 정보를 확인할 수 있지만, 간단하므로 쉽게 비교할 수 있다.
- 해당 플롯을 통해 '더 좋은 품질의 다이아몬드가 평균적으로 더 저렴하다'는 직관에 반하는 사실을 뒷받침한다.
2.2.reorder()
- 대부분의 범주형 변수에는 고유한 순서가 없음
--> 순서를 변경하여 더 유용한 정보를 주도록 표현할 수 있음
---> 이를 위한 한 가지 방법은 reorder()함수를 사용하는 것
ex) mpg dataset의 class변수를 살펴보고싶다.
- 자동차 조율에 따라 고속도로 주행 거리(hwy)가 어떻게 달라지는지 알아보고자 한다.
ggplot(data = mpg, mapping = aes(x = class, y = hwy)) +
geom_boxplot()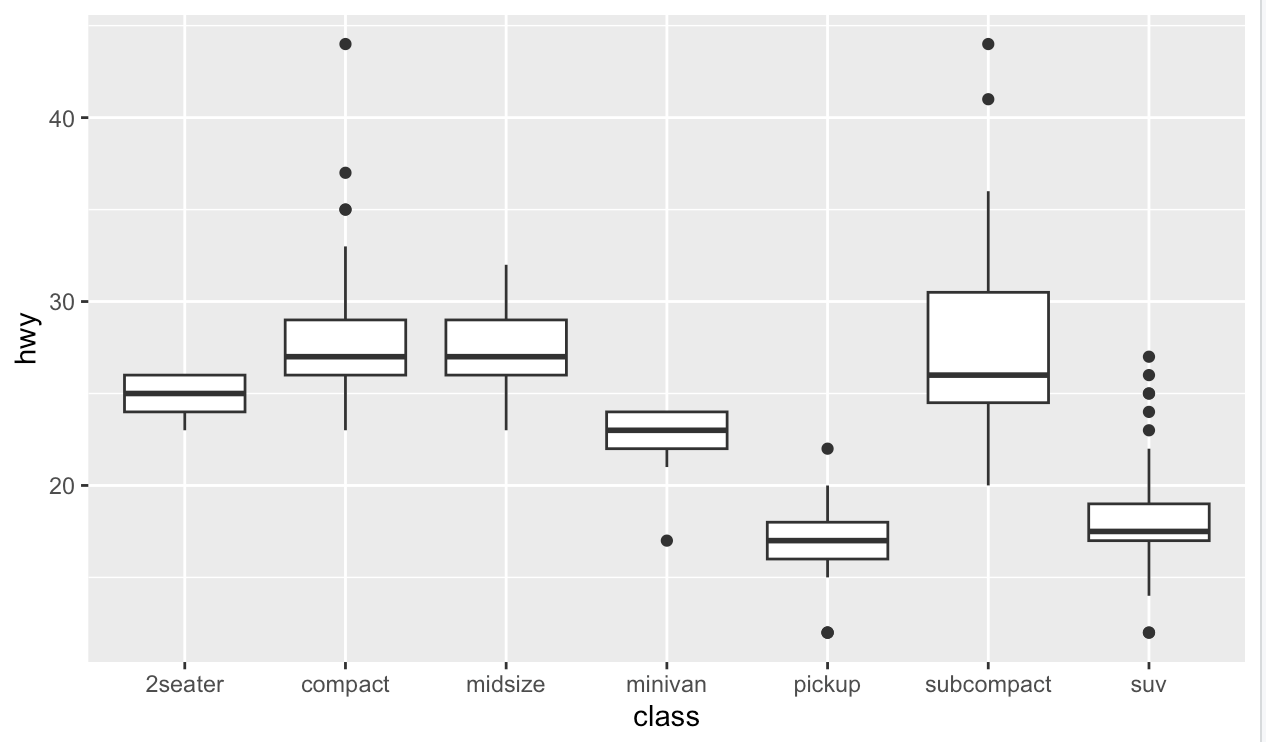
- 순서가 일관되어 있지 않기 때문에 한눈에 분석하기 어려움이있다.
- 더 쉽게 파악하기 위해 hwy변수의 중간값을 기준으로 class변수의 순서를 변경할 수 있음
- 즉 reorder()함수를 이용하면 쉽게 해결할수있다.
reorder(factor, x, FUN = median)- factor : 재정렬할 범주형 변수의 이름
- x : 기준값이 되는 연속형 변수
- FUN : 'x'를 기준으로 'factor'를 재정렬하는 함수를 지정
ex)
ggplot(data = mpg) +
geom_boxplot(
mapping = aes(
x = reorder(class,hwy, FUN = median),
y = hwy
)
)
2.3. 연습문제
Q1) 취소된 항공편과 취소되지 않은 항공편의 출발 시각을 시각화했던 플롯을 개선하기 위해 배운 내용을 사용해보자.
flights %>%
mutate(
cancelled = is.na(dep_time),
sched_hour = sched_dep_time %/% 100,
sched_min = sched_dep_time %% 100,
sched_dep_time = sched_hour + sched_min /60
) %>%
ggplot(mapping = aes(sched_dep_time)) +
geom_freqpoly(
mapping = aes(color = cancelled),
binwidth = 1/4
)
- 취소한 그룹의 빈도수가 상대적으로 적기 때문에 분포를 비교하기 적합하지 않다.
- boxplot을 이용해 비교해주면 된다.
flights %>%
mutate(
cancelled = is.na(dep_time),
sched_hour = sched_dep_time %/% 100,
sched_min = sched_dep_time %% 100,
sched_dep_time = sched_hour + sched_min /60
) %>%
ggplot(mapping = aes(sched_dep_time)) +
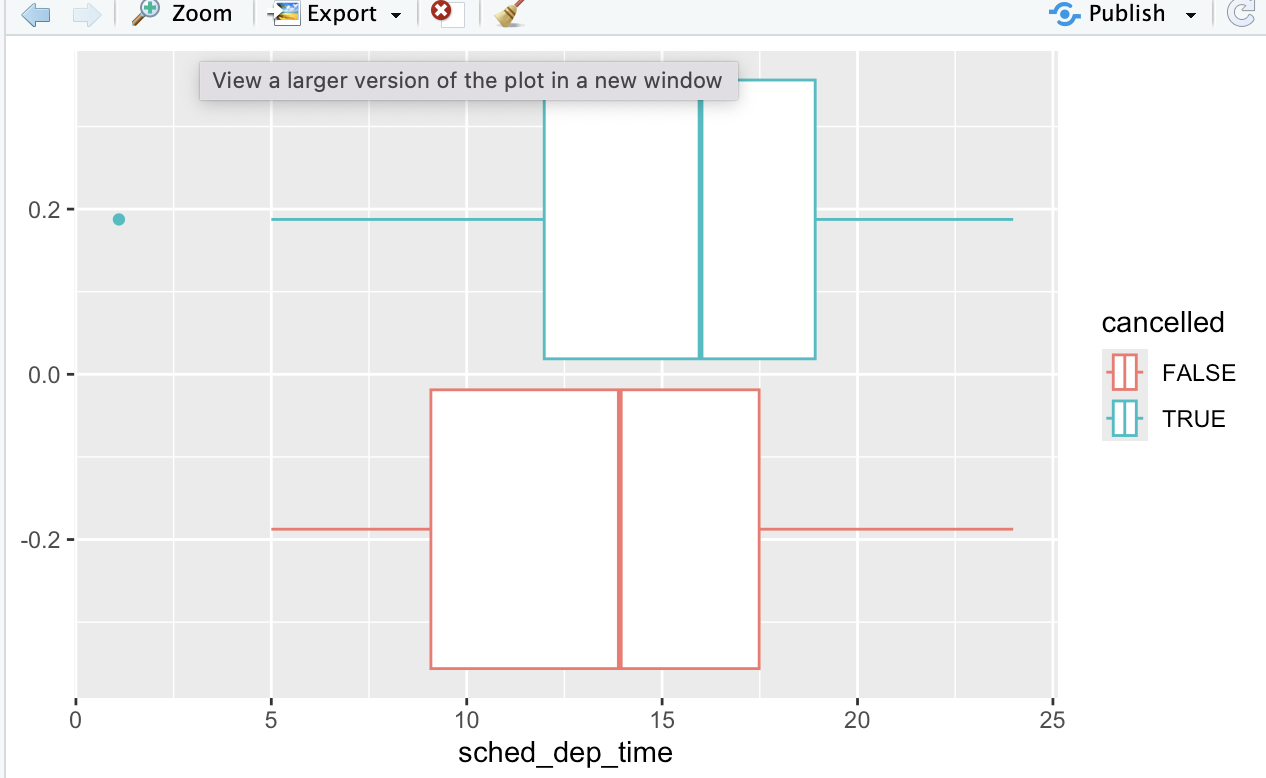
geom_boxplot(
mapping = aes(color = cancelled),
)
Q2) 다이아몬드 데이터셋의 어떤 변수가 다이아몬드의 가격을 예측하는데 가장 중요한가? 그 변수가 color 변수와 상관관계가 있는가?
ggplot(data = diamonds) +
geom_smooth(mapping = aes(x = price , y = carat,color = color))
- 다음과 같이 price는 carat과 우상향관계에 있음을 알수있고,
- color에 따라서 같은 price 대비 carat이 달라진다는 것을 알수 있다.
Q3) 상자 플롯은 데이터셋의 크기가 매우 작았던 시대에 개발되었기 때문에, '이상값'들을 너무 많이 표시하게 된다는 단점이 있다. 이 문제를 해결하기 위한 한 가지 방법은 문자 값 플롯이다. lvplot 패키지를 설치하고 geom_lv()를 사용하여 컷팅에 따른 가격의 분포를 나타내보자. 무엇을 배울수 있는가? 이 플롯을 어떻게 해석하겠는가?
ggplot(data = diamonds, aes(x=cut,y= price)) +
geom_lv()
- 대형 dataset을 4분위수를 넘어 분석하게 해줄수 있게한다.
3. 두 개의 범주형 변수
- 범주형 변수들의 공변동을 시각화하려면 각 조합에 대한 관측값의 수를 세어야한다.
- 이를 위한 한 가지 방법은 내장된 함수인 geom_count()를 이용하는 것이다.
ggplot(data = diamonds) +
geom_count(mapping = aes(x=cut,y = color))
- 플롯에서 원의 크기는 각 값의 조합에서 발생한 관측값의 수를 나타냄
- 공변동은 특정 x값과 y값 사이에 강한 상관관계로 나타날 것이다.
- 또 다른 방법은 dplyr로 빈도수를 계산하는 것이다.
diamonds %>%
count(color, cut)# A tibble: 35 × 3
color cut n
<ord> <ord> <int>
1 D Fair 163
2 D Good 662
3 D Very Good 1513
4 D Premium 1603
5 D Ideal 2834
6 E Fair 224
7 E Good 933
8 E Very Good 2400
9 E Premium 2337
10 E Ideal 3903
# ℹ 25 more rows
# ℹ Use `print(n = ...)` to see more rows- 그후 geom_tile() 함수와 Fill 심미성으로 시각화한다.
diamonds %>%
count(color,cut) %>%
ggplot(mapping = aes(x=color , y = cut)) +
geom_tile(mapping = aes(fill = n))
3.1 연습문제
Q1) 색상 내에서의 컷팅의 분포 또는 컷팅 내에서 색상의 분포를 좀 더 명확하게 보여주기 위해서 데이터셋의 count값을 어떻게 조정할 수 있는가?
diamonds %>%
count(color,cut) %>%
group_by(color) %>%
mutate(prop = n / sum(n)) %>%
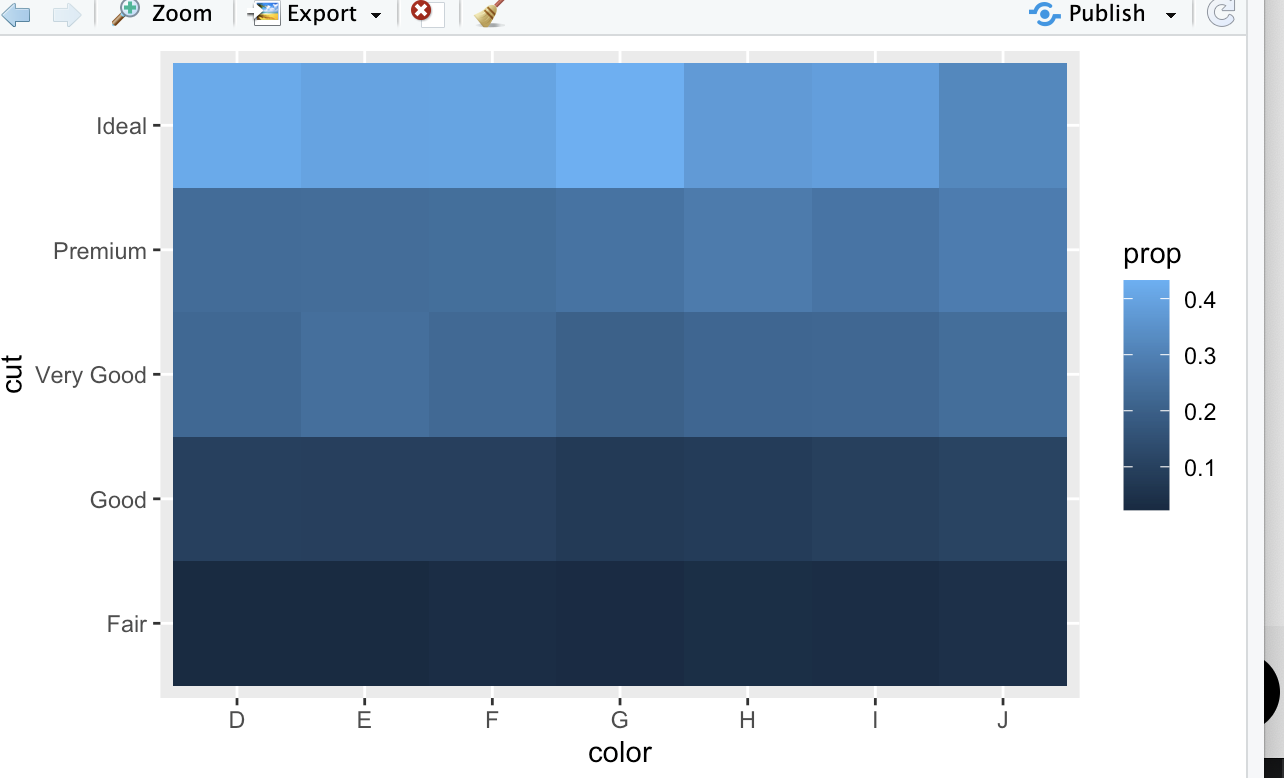
ggplot(mapping = aes(x=color , y = cut)) +
geom_tile(mapping = aes(fill = prop))- group_by(color) 를 통해 color 그룹내의 cut그룹의 데이터를 바탕으로 prop을 계산해준다.
4. 두 개의 연속형 변수
- 두 개의 연속형 변수 사이의 공변동을 시각화하는
- geom_point()
- 연속형 변수중 하나를 그룹화 하여 범주형 변수처럼 만드는 것
