-
0. Reference
-
1. Introduction
-
2. Gradient Descent Variants
-
2.1. Batch Gradient Descent
-
2.2. Stochastic Gradient Descent
-
2.3. Mini-batch Gradient Descent
-
3. Challenges
-
3.1. 적절한 Learning Rate 선택
-
3.2. Learning rate schedules
-
3.3. 모든 파라미터 업데이트에 동일한 Learning Rate 적용 문제
-
3.4. Global Minimum에 미달
-
4. Gradient Descent Optimization algorithms
-
4.1. Momentum
-
4.2. Nesterov Accelerated Gradient(NAG)
-
4.3. Adagrad
-
4.4. Adadelta
-
4.5. RMSProp
-
4.6. Adam(Adaptive Moment Estimation)
-
4.7. AdaMax
-
4.8. Nadam
-
4.9. Visualization of algorithms
-
4.10. Which optimizer to use?
0. Reference
https://arxiv.org/abs/1609.04747
An overview of gradient descent optimization algorithms
Gradient descent optimization algorithms, while increasingly popular, are often used as black-box optimizers, as practical explanations of their strengths and weaknesses are hard to come by. This article aims to provide the reader with intuitions with rega
arxiv.org
1. Introduction
- Gradient Descent는 최적화를 수행하는 가장 인기 있는 알고리즘 중 하나이며, 신경망을 최적화하는 대 있어 가장 일반적으로 사용되는 방법이다.
- 하지만 이러한 알고리즘들은 설명이 부족했기 때문에 Black-box Optimizer Algorithms이라고도 불렸다.
- Gradient Descent는 Loss Function의 Global min을 향해 달려가게 해준다.
2. Gradient Descent Variants
2.1. Batch Gradient Descent
- Vanilla Gradient Descent라고도 불리는 Batch Gradient Descent는 전체 학습 데이터셋에 대한 Loss Function의 Gradient의 평균을 업데이트 하는 것을 의미한다.

- 단 한 번의 업데이트를 수행하기 위해 전체 데이터셋에 대한 그래디언트를 계산해야하므로,
- 매우 느리고 빅데이터를 다룰 경우 실행이 비효율적이다.
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
2.2. Stochastic Gradient Descent
- BGD와 다르게 데이터 한개당 한번씩 Update를 하는 방식이라고 생각하면 된다.

- SGD는 상대적으로 빠르게 작동하지만, 높은 분산을 가지게되며 다음과 같이 파라미터가 요동치게 된다(수렴하진않음).
- 하지만 BGD와 종착지가 거의 유사하다.

for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function,example,params)
params = prams - learning_rate*params_grad
2.3. Mini-batch Gradient Descent
- MBGD는 SGD를 배치처리해서 Mini-batch에서의 gradient 평균을 구해 update하는 것과 같다.
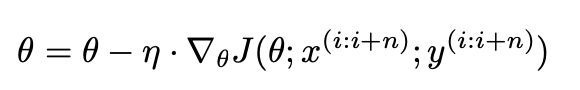
- SGD와 비슷하게 빠른속도로 종착지에 도달하게되며, SGD에 비해 덜 요동치게 된다.
- (더 안정적인 update -> 상대적으로 분산이 작음)
3. Challenges
- 위에서 알아봤던 3가지의 Gradient Descent는 Global Minimum에 도달한다는 것을 보장하긴 어렵다.
- 그래서 다음과 같은 도전과제를 해결해야한다.
3.1. 적절한 Learning Rate 선택
- Learning Rate가 너무 작으면 수렴 속도가 매우 느려지고, 너무 크면 발산하게되어 학습에 방해된다.
3.2. Learning rate schedules
- Learning rate schedule을 사용하여 학습 도중 Learning rate를 조정할 수 있다.
- 사전 정의된 schedule에 따라 learning rate를 감소시키거나
- 매 epoch마다 Loss가 임계값 아래로 떨어지면 learning rate를 감소시킬수 있다.
- 하지만 이 방식은 사전에 정의해야하므로 데이터셋의 특성에 적응하기 힘들다.
3.3. 모든 파라미터 업데이트에 동일한 Learning Rate 적용 문제
- 데이터가 sparse하거나 feature간 빈도가 매우 다를 경우, 각각의 feature에 서로다른 가중치를 주고 싶을 것이다.
3.4. Global Minimum에 미달
- local minima나 saddle point에 빠질 확률이 크다. 그래서 이를 탈출 시켜줘야 한다.
4. Gradient Descent Optimization algorithms
- 해당 파트에선 앞에 말했던 도전 과제를 해결하기 위해 나온 Optimizer들을 소개하게 된다.
4.1. Momentum
- SGD는 기울기가 가파른 곳에서 최적값을 향해 잘 찾아가지 못한다.
- 이는 보통 local minima나 saddle point 부근에 흔히 나타나게 된다.
- 이러한 상황에서 되게 진동하게 된다.(사진 참조)

- 하지만 Momentum은 SGD가 관련된 방향으로 더 빠르게 이동하도록 돕고, 진동을 줄여준다.

- 이전 단계의 업데이트된 벡터에 Momentum rate를 곱해줘 업데이틀 하게 된다.
- 마치 관성을 추가한 거라고 생각해도 좋다.(수식은 다음과 같다.)

- 이러한 Momentum은 마치 언덕 아래로 공을 굴리는 것과 같다.
- 공은 언덕을 내려가면서 운동량을 축적하며 점점 빨라지게 된다.(관성)
- 그래서 Gradient가 계속 같은 방향을 가리키는 차원에선 계속 속도가 빨라지고
- 방향이 바뀌는 차원에선 속도가 느려지게 된다.
4.2. Nesterov Accelerated Gradient(NAG)
- Momentum에 사용했던 공이 지능이 생기면 어떨까?
- 즉, 매순간 최선의 선택을 하게끔 설정해주는 것을 의미한다.
- 공이 자신의 이동 방향을 어느 정도 파악하여 언덕이 다시 오르막으로 변하기 전에 속도를 늦추도록 하는 것이다.
- 이를 바탕으로 Nesterov Accelerated Gadient(NAG)라는 알고리즘을 구현이 됐다.
- 모멘텀 항에 이러한 예측 능력을 부여하는 방법이라고 생각하면 된다.
- 미리 관성방향으로 움직이고 그 후 그 자리에서의 최선의 방향으로 이동하는 것을 의미한다.
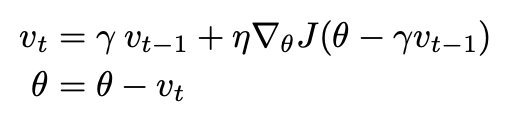

cf) Blue : Momentum, Green : NAG , Orange + Red : NAG의 상세 경로
4.3. Adagrad
- 일정한 Learning rate를 사용하지 않고 변수마다그리고 스텝마다 learning rate가 바뀐다.
- 시간이 지날수록 learning rate는 줄어드는데 큰 변화를 겪은 변수의 learning rate는 대폭 작아지고
- 작은 변화를 겪은 변수의 learning rate는 소폭으로 작아진다.
- 이러한 논리는 큰 변화를 겪은 변수는 이미 최적에 가까워졌고 작은 변화를 겪은 변수는 최적에 아직 멀다고 생각하기 때문이다.
- 점화식은 다음과 같다.

- hn은 누적합이기때문에 점점 시간이 지나면 지날수록 커지게 된다.
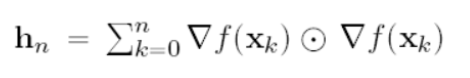
- 그렇기 때문에 점점 학습이 느려지게 된다.(Iearning rate가 감소하기 때문이다.)
4.4. Adadelta
- AdaDelta는 AdaGrad의 누적합이 계속 커지는 현상을 방지하기 위해서 고안되었다.
- 이를 위해 AdaDelta는 가중평균(exponentially weighted averge)을 이용한다.
- 여기서 rate는 0.9로 잡아둔다. 즉, 과거에 대한 비중을 크게 둔다는 것을 의미한다.

- 바로 다음으로 볼 RMSProp과의 차이는 Adadelta는 Learning rate가 없다는 것이다.
4.5. RMSProp
- RMSprop은 논문으로 발표가 된 Optimizer가 아니고 Hinton교수가 Coursera에서 제안한 방식이라고 한다.
- Adagrad에서 hn을 단순히 누적합으로 생각하는 것이 아닌 가중평균으로 생각하여 과거에 집중하여 다른 값에 수렴하게 만들어준다.

4.6. Adam(Adaptive Moment Estimation)
- Adam은 Momentum과 RMSProp을 합친것과 같다고 볼 수 있다.

- 여기서 betta1,betta2값이 1에 가까우면 가까울수록 m,v가 0에 편향된다는 것을 관찰했기에
- 이를 다음과 같이 보정해준다.

- 최종적인 Adam식은 다음과 같다.

- 이러한 Adam은 보편적인 상황에서 효율이 잘나오는 Optimizer라고 한다.
4.7. AdaMax
- AdaMax는 Adam에서의 RMSProp부분의 norm을 무한대라고 생각하고 나오게 된것이다.
- 기존의 Adam에서의 RMSProp부분은 norm은 2라고 둘 수 있다.(제곱)
- 여기서 제곱대신 p라고 일반화을 해보자.

- p라고 두면 사실 계산하기 힘들다. 하지만, p -> infinity로 극한을 보내면 다음과 같이 단순화된다.

- 결과적으론 다음과 같은 AdaMax가 나오게 된다.

4.8. Nadam
- 기존의 Adam이 Momentum과 RMSProp이 합쳐진 알고리즘이라면,
- Nadam은 NAG와 RMSProp이 합쳐진 알고리즘이다.
- NAG가 Momentum보다 더 효율적이라는 생각하에 나오게 된거라고 생각하면 된다.
- 식유도도 Momentum대신 NAG를 넣어서 생각하면 된다.

4.9. Visualization of algorithms

4.10. Which optimizer to use?
- 한줄로 요약하자면 Adam과 비슷한 Adaptive learning-rate method를 사용하는게 보편적으로 좋다고 한다.
'Paper Review(논문 리뷰) > Deep Learning' 카테고리의 다른 글
0. Reference
https://arxiv.org/abs/1609.04747
An overview of gradient descent optimization algorithms
Gradient descent optimization algorithms, while increasingly popular, are often used as black-box optimizers, as practical explanations of their strengths and weaknesses are hard to come by. This article aims to provide the reader with intuitions with rega
arxiv.org
1. Introduction
- Gradient Descent는 최적화를 수행하는 가장 인기 있는 알고리즘 중 하나이며, 신경망을 최적화하는 대 있어 가장 일반적으로 사용되는 방법이다.
- 하지만 이러한 알고리즘들은 설명이 부족했기 때문에 Black-box Optimizer Algorithms이라고도 불렸다.
- Gradient Descent는 Loss Function의 Global min을 향해 달려가게 해준다.
2. Gradient Descent Variants
2.1. Batch Gradient Descent
- Vanilla Gradient Descent라고도 불리는 Batch Gradient Descent는 전체 학습 데이터셋에 대한 Loss Function의 Gradient의 평균을 업데이트 하는 것을 의미한다.

- 단 한 번의 업데이트를 수행하기 위해 전체 데이터셋에 대한 그래디언트를 계산해야하므로,
- 매우 느리고 빅데이터를 다룰 경우 실행이 비효율적이다.
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
2.2. Stochastic Gradient Descent
- BGD와 다르게 데이터 한개당 한번씩 Update를 하는 방식이라고 생각하면 된다.

- SGD는 상대적으로 빠르게 작동하지만, 높은 분산을 가지게되며 다음과 같이 파라미터가 요동치게 된다(수렴하진않음).
- 하지만 BGD와 종착지가 거의 유사하다.

for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function,example,params)
params = prams - learning_rate*params_grad
2.3. Mini-batch Gradient Descent
- MBGD는 SGD를 배치처리해서 Mini-batch에서의 gradient 평균을 구해 update하는 것과 같다.
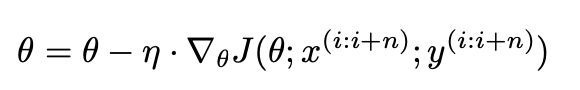
- SGD와 비슷하게 빠른속도로 종착지에 도달하게되며, SGD에 비해 덜 요동치게 된다.
- (더 안정적인 update -> 상대적으로 분산이 작음)
3. Challenges
- 위에서 알아봤던 3가지의 Gradient Descent는 Global Minimum에 도달한다는 것을 보장하긴 어렵다.
- 그래서 다음과 같은 도전과제를 해결해야한다.
3.1. 적절한 Learning Rate 선택
- Learning Rate가 너무 작으면 수렴 속도가 매우 느려지고, 너무 크면 발산하게되어 학습에 방해된다.
3.2. Learning rate schedules
- Learning rate schedule을 사용하여 학습 도중 Learning rate를 조정할 수 있다.
- 사전 정의된 schedule에 따라 learning rate를 감소시키거나
- 매 epoch마다 Loss가 임계값 아래로 떨어지면 learning rate를 감소시킬수 있다.
- 하지만 이 방식은 사전에 정의해야하므로 데이터셋의 특성에 적응하기 힘들다.
3.3. 모든 파라미터 업데이트에 동일한 Learning Rate 적용 문제
- 데이터가 sparse하거나 feature간 빈도가 매우 다를 경우, 각각의 feature에 서로다른 가중치를 주고 싶을 것이다.
3.4. Global Minimum에 미달
- local minima나 saddle point에 빠질 확률이 크다. 그래서 이를 탈출 시켜줘야 한다.
4. Gradient Descent Optimization algorithms
- 해당 파트에선 앞에 말했던 도전 과제를 해결하기 위해 나온 Optimizer들을 소개하게 된다.
4.1. Momentum
- SGD는 기울기가 가파른 곳에서 최적값을 향해 잘 찾아가지 못한다.
- 이는 보통 local minima나 saddle point 부근에 흔히 나타나게 된다.
- 이러한 상황에서 되게 진동하게 된다.(사진 참조)

- 하지만 Momentum은 SGD가 관련된 방향으로 더 빠르게 이동하도록 돕고, 진동을 줄여준다.

- 이전 단계의 업데이트된 벡터에 Momentum rate를 곱해줘 업데이틀 하게 된다.
- 마치 관성을 추가한 거라고 생각해도 좋다.(수식은 다음과 같다.)

- 이러한 Momentum은 마치 언덕 아래로 공을 굴리는 것과 같다.
- 공은 언덕을 내려가면서 운동량을 축적하며 점점 빨라지게 된다.(관성)
- 그래서 Gradient가 계속 같은 방향을 가리키는 차원에선 계속 속도가 빨라지고
- 방향이 바뀌는 차원에선 속도가 느려지게 된다.
4.2. Nesterov Accelerated Gradient(NAG)
- Momentum에 사용했던 공이 지능이 생기면 어떨까?
- 즉, 매순간 최선의 선택을 하게끔 설정해주는 것을 의미한다.
- 공이 자신의 이동 방향을 어느 정도 파악하여 언덕이 다시 오르막으로 변하기 전에 속도를 늦추도록 하는 것이다.
- 이를 바탕으로 Nesterov Accelerated Gadient(NAG)라는 알고리즘을 구현이 됐다.
- 모멘텀 항에 이러한 예측 능력을 부여하는 방법이라고 생각하면 된다.
- 미리 관성방향으로 움직이고 그 후 그 자리에서의 최선의 방향으로 이동하는 것을 의미한다.
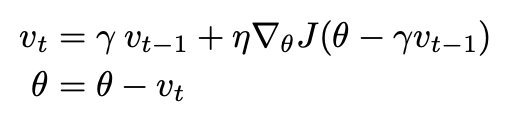

cf) Blue : Momentum, Green : NAG , Orange + Red : NAG의 상세 경로
4.3. Adagrad
- 일정한 Learning rate를 사용하지 않고 변수마다그리고 스텝마다 learning rate가 바뀐다.
- 시간이 지날수록 learning rate는 줄어드는데 큰 변화를 겪은 변수의 learning rate는 대폭 작아지고
- 작은 변화를 겪은 변수의 learning rate는 소폭으로 작아진다.
- 이러한 논리는 큰 변화를 겪은 변수는 이미 최적에 가까워졌고 작은 변화를 겪은 변수는 최적에 아직 멀다고 생각하기 때문이다.
- 점화식은 다음과 같다.

- hn은 누적합이기때문에 점점 시간이 지나면 지날수록 커지게 된다.
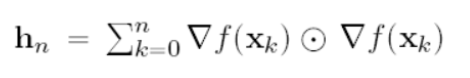
- 그렇기 때문에 점점 학습이 느려지게 된다.(Iearning rate가 감소하기 때문이다.)
4.4. Adadelta
- AdaDelta는 AdaGrad의 누적합이 계속 커지는 현상을 방지하기 위해서 고안되었다.
- 이를 위해 AdaDelta는 가중평균(exponentially weighted averge)을 이용한다.
- 여기서 rate는 0.9로 잡아둔다. 즉, 과거에 대한 비중을 크게 둔다는 것을 의미한다.

- 바로 다음으로 볼 RMSProp과의 차이는 Adadelta는 Learning rate가 없다는 것이다.
4.5. RMSProp
- RMSprop은 논문으로 발표가 된 Optimizer가 아니고 Hinton교수가 Coursera에서 제안한 방식이라고 한다.
- Adagrad에서 hn을 단순히 누적합으로 생각하는 것이 아닌 가중평균으로 생각하여 과거에 집중하여 다른 값에 수렴하게 만들어준다.

4.6. Adam(Adaptive Moment Estimation)
- Adam은 Momentum과 RMSProp을 합친것과 같다고 볼 수 있다.

- 여기서 betta1,betta2값이 1에 가까우면 가까울수록 m,v가 0에 편향된다는 것을 관찰했기에
- 이를 다음과 같이 보정해준다.

- 최종적인 Adam식은 다음과 같다.

- 이러한 Adam은 보편적인 상황에서 효율이 잘나오는 Optimizer라고 한다.
4.7. AdaMax
- AdaMax는 Adam에서의 RMSProp부분의 norm을 무한대라고 생각하고 나오게 된것이다.
- 기존의 Adam에서의 RMSProp부분은 norm은 2라고 둘 수 있다.(제곱)
- 여기서 제곱대신 p라고 일반화을 해보자.

- p라고 두면 사실 계산하기 힘들다. 하지만, p -> infinity로 극한을 보내면 다음과 같이 단순화된다.

- 결과적으론 다음과 같은 AdaMax가 나오게 된다.

4.8. Nadam
- 기존의 Adam이 Momentum과 RMSProp이 합쳐진 알고리즘이라면,
- Nadam은 NAG와 RMSProp이 합쳐진 알고리즘이다.
- NAG가 Momentum보다 더 효율적이라는 생각하에 나오게 된거라고 생각하면 된다.
- 식유도도 Momentum대신 NAG를 넣어서 생각하면 된다.

4.9. Visualization of algorithms

4.10. Which optimizer to use?
- 한줄로 요약하자면 Adam과 비슷한 Adaptive learning-rate method를 사용하는게 보편적으로 좋다고 한다.
