1. Derivation of this classification
- 우리는 Lecture 6 에서 SVM에 대해서 간단하게 알아보았다.
- classifier은 다음과 같이 출력하게 된다.

- 여기서 우리의 목적은 w,b를 찾아내는 것을 의미한다.
- 가장 Optimal한 Solution을 찾기 위해서 다음 조건을 만족해야 한다.
- 밑의 최악의 경우의 Gamma가 최대가 되도록 해야한다.
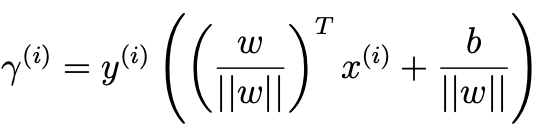
- 여기서 ||w||는 크기가 어떻게 나오더라도 직선자체는 변하지 않는다.
- 그래서, 우리는 이러한 사실을 바탕으로 식조작이 편하게 고쳐줄 수 있다.
- 그래서 ||w|| = 1 / gamma라고 둬보자.
- 그러면 우리가 목표하고자 하는 건 다음과 같다.
max( gamma) = max(1 / ||w||) 이기 때문에

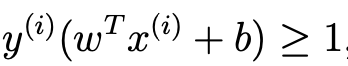
- max(gamma)를 한다는 반대로 다음과 같이 생각할 수 있다.
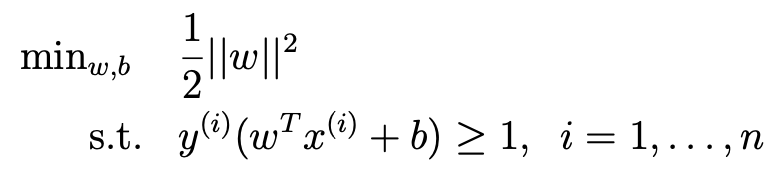
- 이를 랑그랑주 승수법을 이용하여 한번 w를 찾아보자.
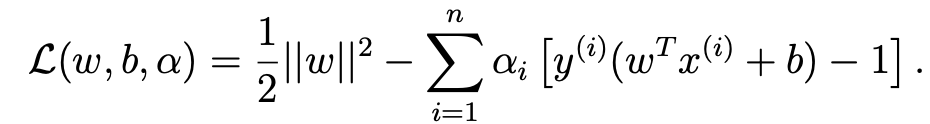
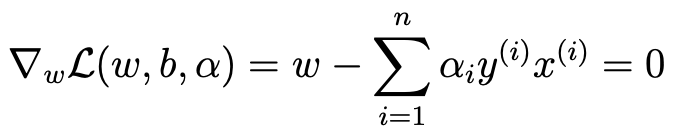
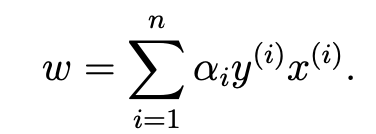
- 이 결과를 토대로 다시 한번 밑의 식(두 개)를 정리해보자.
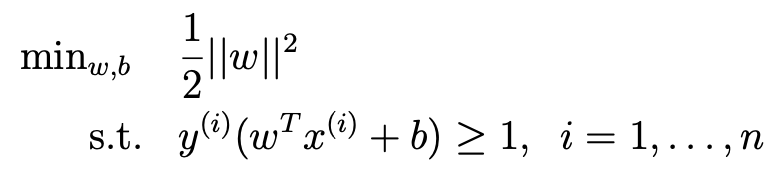
- 위에 있는 1번식을 정리하면 다음과 같다.

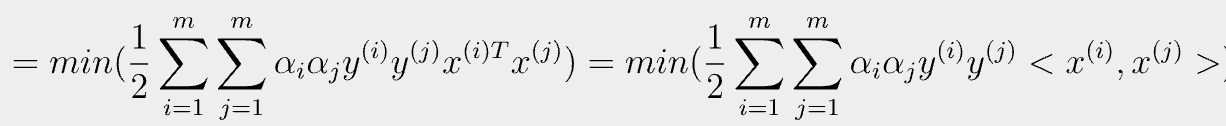
- 2번식을 정리하면 다음과 같다.
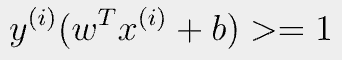
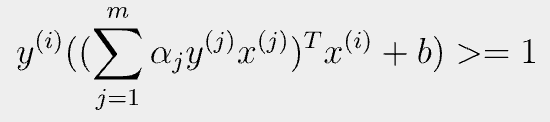
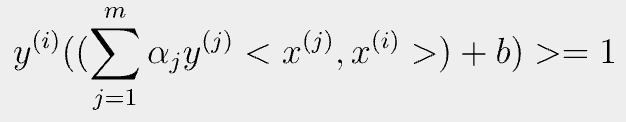
- 1번,2번식을 최종적으로 정리하게 된 꼴을 보게 되면 inner product가 공통으로 존재하는 걸 알 수 있다.
- feature vector가 곱해진 꼴인데, infinity-dimension을 가진 vector도 처리 가능하다라는 의미를 가진다.
2. The dual Optimization problem
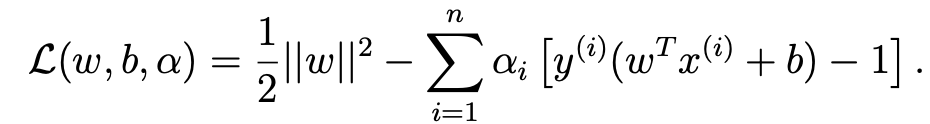
- 해당 식의 sigma부분을 전개해줘서 식정리를 하면 다음과 같다.
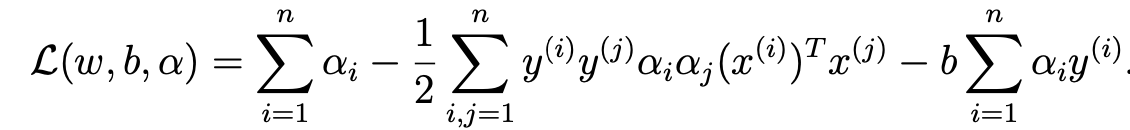
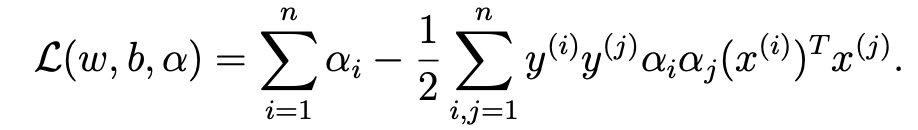
- b가 사라진 이유는 다음과 같다.
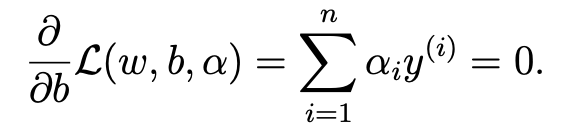
- 따라서 다음과 같은 식이 유도가 된다.

- 일단 여기까지 이해해보고, 다음으로 Kernel을 알아봐보자.
3. Kernel
3.1. Kernel trick
- 우선 Kernel을 알아가기 전에 Kernel trick에 대해 미리 잡고가자.
Step 1) <x^(i),x^(j)>에 대한 알고리즘을 작성
Step 2) x 를 x보다 더 고차원인 phi로 mapping시킨다.
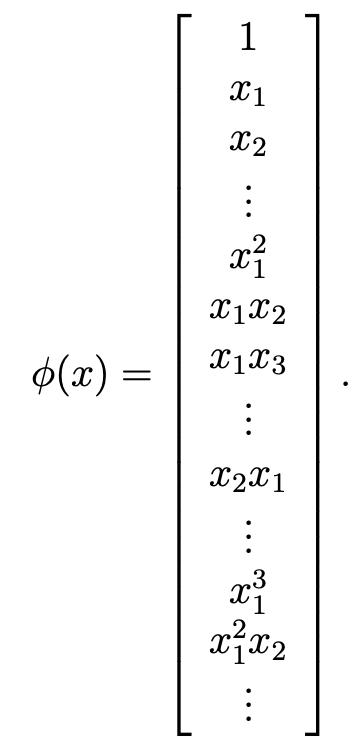
Step 3) K(x^(i),x^(j))= <phi(x),phi(z)>를 계산할 수 있는 지 확인하기
Step 4) <x^(i),x^(j)>에 대한 알고리즘을 K(x^(i),x^(j))로 변경
3.2. Example of Kernels
- 간단하게 커널의 예시를 알아보자.
- x가 다음과 같이 3차원 벡터라고 가정하자
x = [x1,x2,x3]
- 그리고 이에 따른 feature mapping이 9차원 벡터로 주어져있다고 가정하자
phi(x) = [x1x1,x1x2,x1x3,x2x1,x2x2,x2x3,x3x1,x3x2,x3x3]
phi(z) = [z1z1,z1z2,z1z3,z2z1,z2z2,z2z3,z3z1,z3z2,z3z3]
- 사실 이렇게 되면 x의 길이의 제곱만큼의 시간복잡도가 생기게 된다.
- 하지만 이를 Kernel trick으로 생각하면 다음과 같이 x의 길이만큼 시간복잡도가 생긴다는 것을 알 수 있다.
- K(x,z) = <phi(x),phi(z)> = (x^Tz)^2
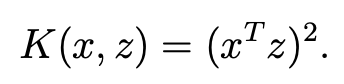
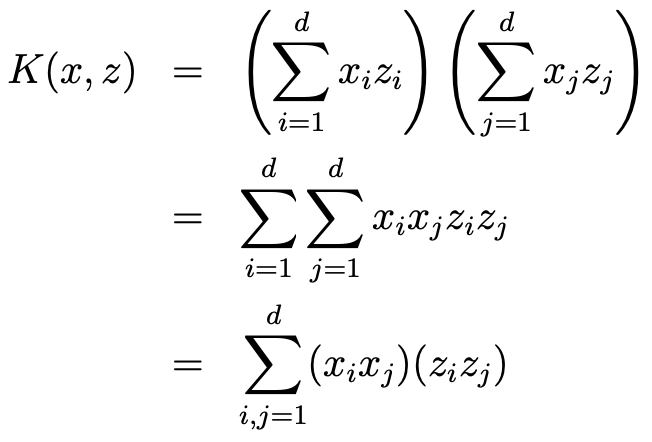
4. SVM
- 여기서 SVM에 대한 정리가 나오게 된다.
- SVM = Optimal Margin Classifier + Kernel trick 이라는 것이다.
- 해당 gif을 보면 이해가 쉬울것이다.

- 2차원으로 존재하던 데이터를 3차원으로 mapping(Kerner trick)하여 Optimal Margin Classifier하게 된다.
- 즉, 고차원에서 데이터를 분류할땐 Linear하게 분류했지만 기존의 데이터 차원의 관점에서 봤을때 nonlinear하게 분류를 할 수 있다.
- 그럼 Kernel은 어떻게 만들수 있을까?
- 우선 여러 가정과 조건이 존재한다.
"""
i) 만약 x,z가 비슷하다면 K(x,z)의 결과가 커야함
ii) 만약 x,z가 다르다면 K(x,z)의 결과가 작아야함
"""
- 마치 벡터의 연산과 동일하게 진행됨을 볼 수 있다.
- 뿐만 아니라 LWR의 공식이 생각이 나게 될 것이다.
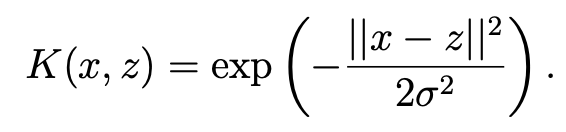
- 이 Kernel을 Gaussian Kernel이라고 불린다. --> 무한대의 Dimension을 갖게 된다.
- 또 다른 Kernel로 Linear Kernel은 다음과 같다.
K(x,z) = x^Tz = <x,z> (cf, 많이 쓰이는 Kernel이라고 한다.)
'DS Study > CS 229(Machine Learning)' 카테고리의 다른 글
| [CS229] [9] Lecture 9 - Approx/Estimation Error & ERM (1) | 2025.02.07 |
|---|---|
| [CS229] [8] Lecture 8 - Data Splits, Models & Cross-Validation (1) | 2025.01.22 |
| [CS 229] [6] Lecture 6 - Support Vector Machines (1) | 2025.01.20 |
| [CS229] [5] Lecture 5 - GDA & Naive Bayes (0) | 2025.01.17 |
| [CS229] [4] Lecture 4 - Perceptron & Generalized Linear Model (0) | 2025.01.14 |
