1. 다차원 배열의 계산
1.1. 다차원 배열
- 다차원 배열은 기본적으로 숫자의 집합이라고 생각하면 편하다.
- 간단히 배열이란 직사각형의 집합이라고 생각하면 된다. 만일 N차원으로 나열된 것이라면 N차원 배열이라고 정의한다.
- 특히 2차원 배열은 행렬(Matrix)라고 부르고, 가로방향을 행, 세로 방향을 열이라고 정의한다.
cf) 3차이상인 배열은 텐서(Tensor)라고 부른다.
- 간단한 코드 예제를 봐보자.
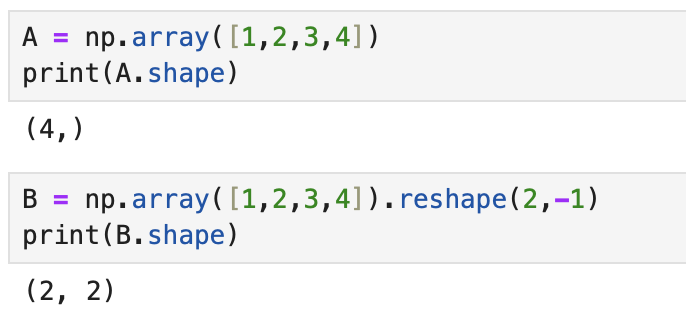
1.2. 행렬 곱
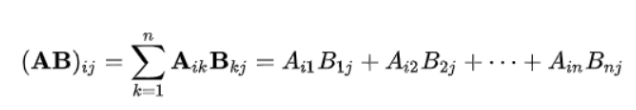
- 이를 예제와 함께 보면 다음과 같다.
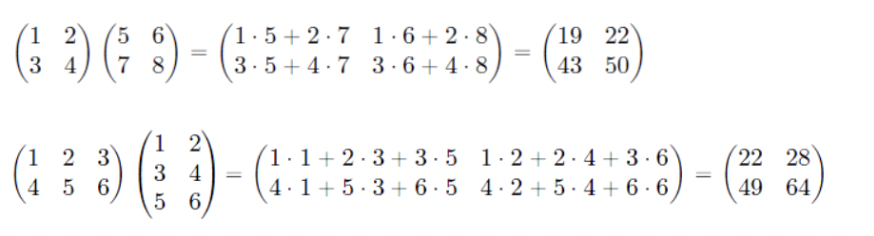
- m x n 행렬과 n x l행렬의 곱은 m x l 행렬이 된다.
- 행렬 곱은 numpy에서 np.dot()을 이용하여 구할 수 있다.
ex)

2. 신경망에서의 행렬 곱
- 신경망과 행렬곱은 무슨 연관이 있을까?
- 다음과 같이 신경망이 주어져 있다고 생각해보자
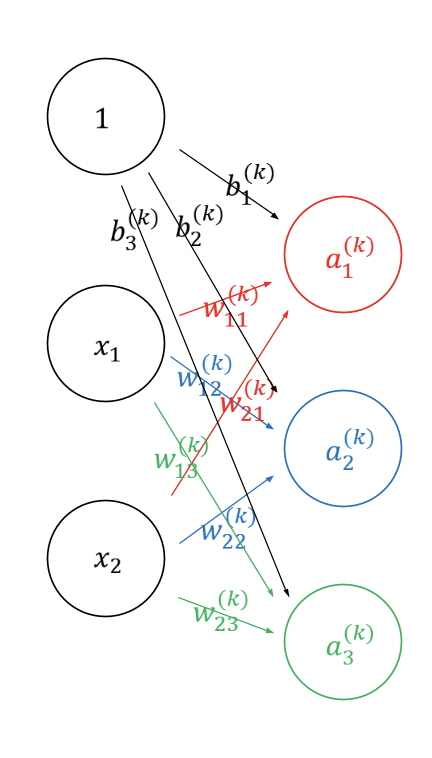
- 이를 식으로 나타내면 다음과 같은 식이 유도될 것이다.

- 이를 행렬 곱으로 나타내면 다음과 같아진다.
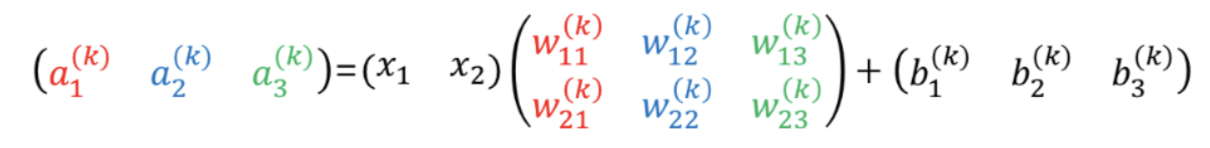
- 이에 관한 내용을 3층 신경망에 대해 빗대어 살펴보자.
3. 3층 신경망 구현하기
3.1. 3층 신경망 구조
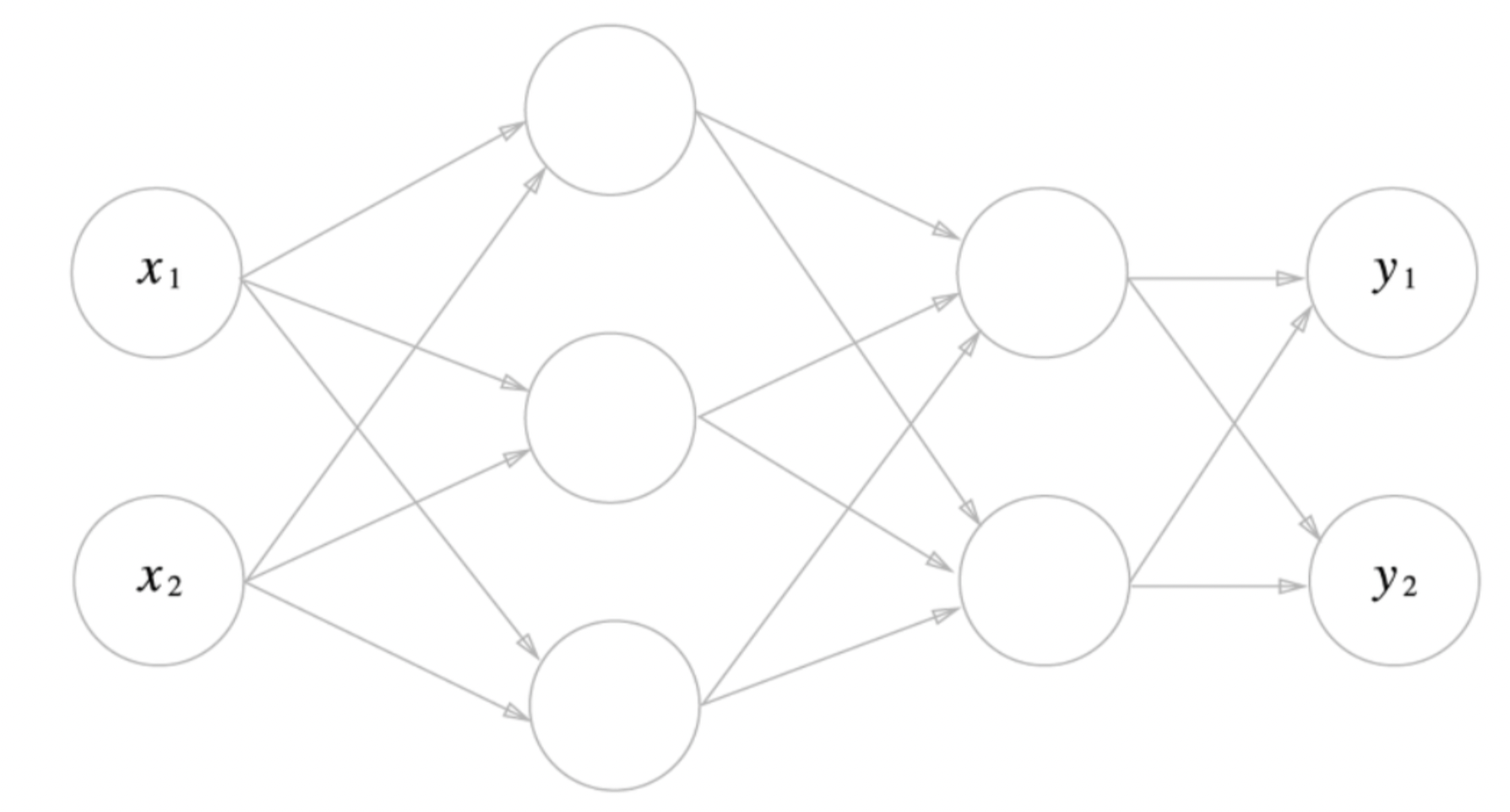
- 이번에 구현하게 될 3층신경망을 설명해보자
- 입력층 (0층) : 2개
- 첫 번째 은닉층(1층) : 3개
- 두 번째 은닉층(2층) : 2개
- 출력층 (3층) : 2개
의 뉴런으로 이루어져 있다. 더 자세한 구조는 점차 알아가보자
3.2. 입력층 -> 1층 구현하기
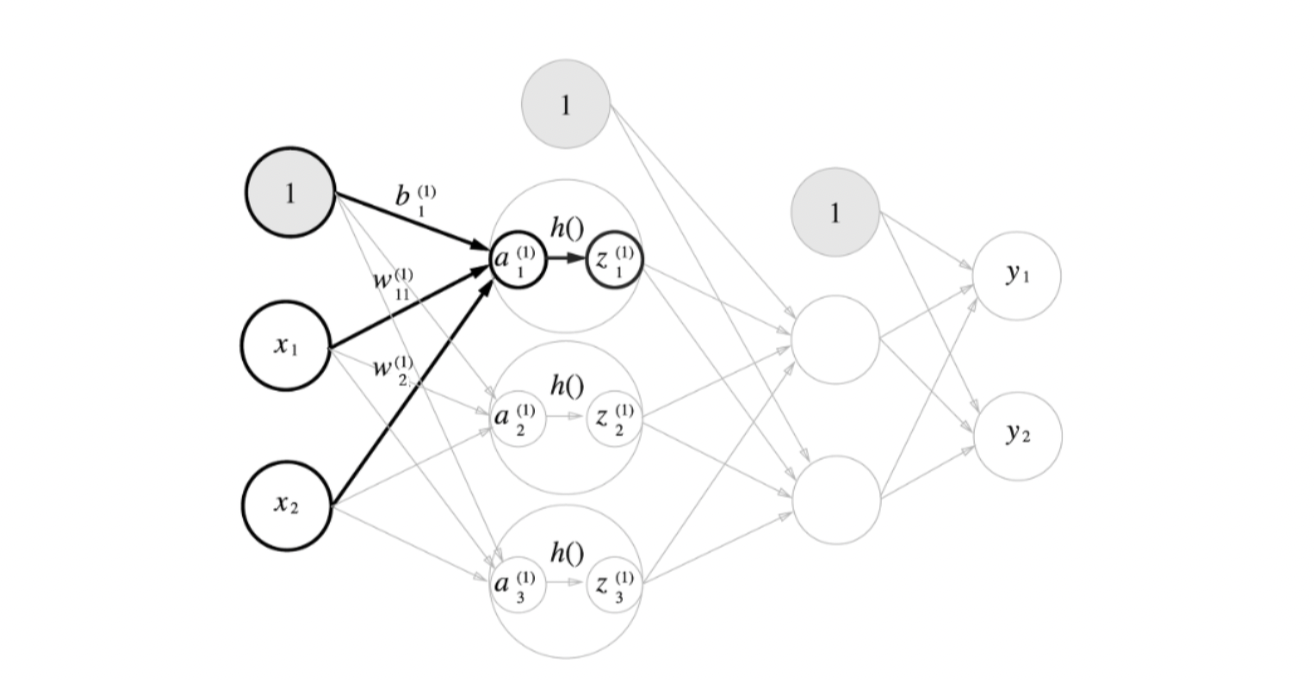
- 이를 행렬곱으로 나타내면 다음과 같다.
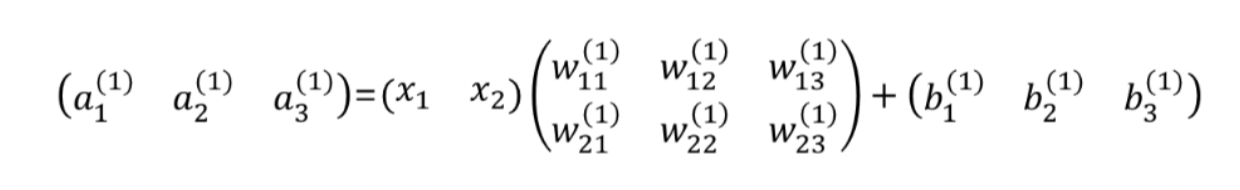
- (z1, z2, z3) = (h(a1) , h(a2), h(a3)) 가 된다. 이를 코드로 구현해보자.(Activation Function는 ReLU라고하자)
Code
X = np.array([1,2])
W1 = np.array([0.1,-0.2,0.3,-0.4,0.5,-0.6]).reshape(2,-1)
b1 = np.zeros(3)
A1 = np.dot(X,W1) + b1
Z1 = ReLU(A1)
Z1
#array([0. , 0.8, 0. ])
3.3. 1층 -> 2층 구현하기
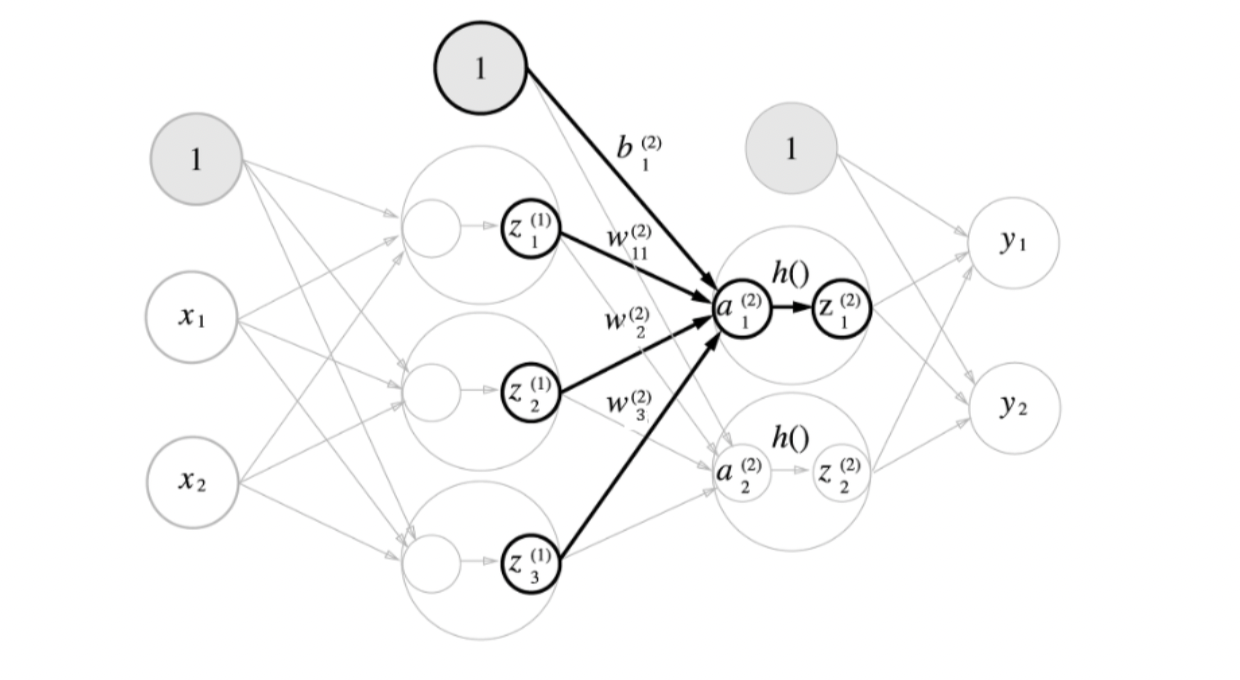
- 이를 행렬곱으로 나타내면 다음과 같다.
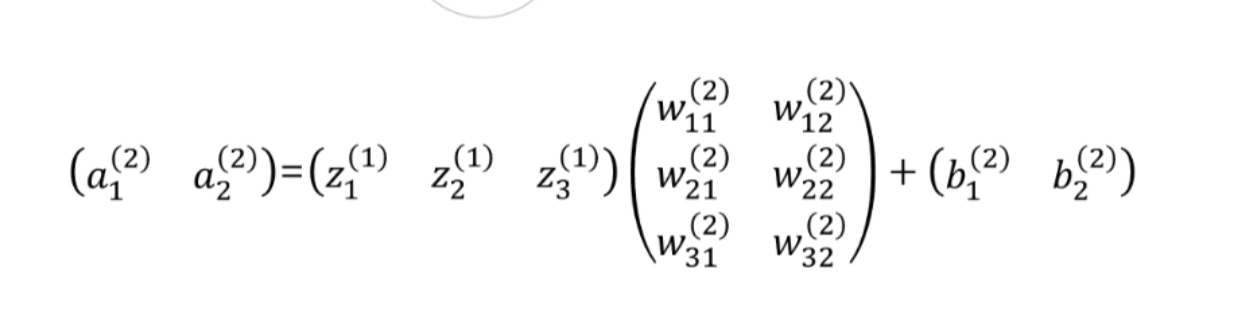
- 이를 코드로 구현해보자.
W2 = np.array([-1,2,3,4,5,-6]).reshape(-1,2)
b2 = np.ones(2)
A2 = np.dot(Z1,W2) + b2
Z2 = ReLU(A2)
Z2 # array([3.4, 4.2])
3.4. 2층 -> 출력층 구현

- 은닉층 -> 출력층의 특징은 마지막에 softmax 함수를 지난다는 것이다.
- SoftMax함수는 이따가 알아보도록 하고 이를 행렬곱으로 나타내면 다음과 같다.
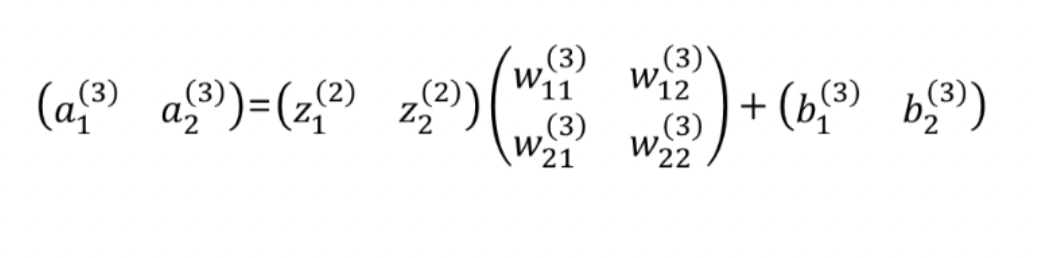
- 코드로 나타내면 다음과 같다.
def softmax(x):
return np.e**x/sum(np.e**x)
W3 = np.array([3,-4,3,-4]).reshape(2,2)
b2 = np.array([1,3])
A3 = np.dot(Z2,W3)+b2
Y = softmax(A3)
Y #array([1.0000000e+00, 5.8092829e-23])
3.5. 구현 정리
- 지금까지 나타낸 던 코드들을 한번에 정리하면 다음과 같다.
def init_network():
network = {}
network['W1'] = np.array([0.1,-0.2,0.3,-0.4,0.5,-0.6]).reshape(2,-1)
network['b1'] = np.zeros(3)
network['W2'] = np.array([-1,2,3,4,5,-6]).reshape(-1,2)
network['b2'] = np.ones(2)
network['W3'] = np.array([3,-4,3,-4]).reshape(2,2)
network['b3'] = np.array([1,3])
return network
def forward(network, x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x,W1) + b1
z1 = ReLU(a1)
a2 = np.dot(z1,W2) + b2
z2 = ReLU(a2)
a3 = np.dot(z2,W3) + b3
y = softmax(a3)
return y
network = init_network()
x = np.array([1,2])
y = forward(network, x)
y
-----------------------------------------------------------------------
#Output
array([1.0000000e+00, 5.8092829e-23])- 여기서 신경망을 dictionary로 저장한 이유는 해시맵 특성상 더 빠른 속도로 불러오는게 가능하기 때문이다.
4.SoftMax
- 앞서서 우리는 마지막 은닉층 -> 출력층으로 갈때 softmax 함수를 이용했었다.
- 이 softmax에 대해서 한번 알아가보자.

- 다음과 같이 exp()를 적용하고 normalize 해줘서 확률벡터로 나타나게 해주는 역할을 하게된다.
4.1. SoftMax 주의점
- softmax를 컴퓨터로 구현할 때 중요한 점은 OverFlow를 방지해줘야 한다는 것이다.
- 기본적으로 exp()를 사용하게 되는데 이는 너무 큰값을 뱉는다는 단점이 있다. -> OverFlow 발생
- 그래서 데이터의 최댓값을 모든 원소마다 빼주고 SoftMax를 진행해주면 된다.
- 이게 가능한 이유는 Softmax의 특징에서 알 수 있다.

- 해당 수식을 직접 SoftMax하게 되면 기존의 (x1,x2,x3)를 softmax한것과 결과값이 같아진다.
- 즉, C = -max(X) 일때도 같은값이 유도된다는 것이다.
- 그래서 컴퓨터에서 OverFlow가 일어나지 않게 코드를 작성하면 다음과 같다
def softmax(x):
x -= max(x)
return np.e**x/sum(np.e**x)
'DS Study > 밑바닥부터 시작하는 딥러닝 1' 카테고리의 다른 글
| [밑시딥1] [5] 손실함수(Loss Function) (0) | 2024.07.29 |
|---|---|
| [밑시딥1] [4] MNIST (0) | 2024.07.29 |
| [밑시딥1] [2] 활성화함수 (Activation Function) (0) | 2024.07.26 |
| [밑시딥1] [1] 퍼셉트론 (Perceptron) (0) | 2024.07.24 |
1. 다차원 배열의 계산
1.1. 다차원 배열
- 다차원 배열은 기본적으로 숫자의 집합이라고 생각하면 편하다.
- 간단히 배열이란 직사각형의 집합이라고 생각하면 된다. 만일 N차원으로 나열된 것이라면 N차원 배열이라고 정의한다.
- 특히 2차원 배열은 행렬(Matrix)라고 부르고, 가로방향을 행, 세로 방향을 열이라고 정의한다.
cf) 3차이상인 배열은 텐서(Tensor)라고 부른다.
- 간단한 코드 예제를 봐보자.

1.2. 행렬 곱
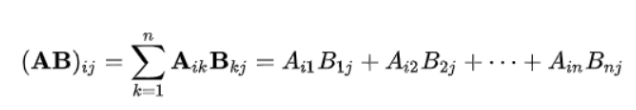
- 이를 예제와 함께 보면 다음과 같다.
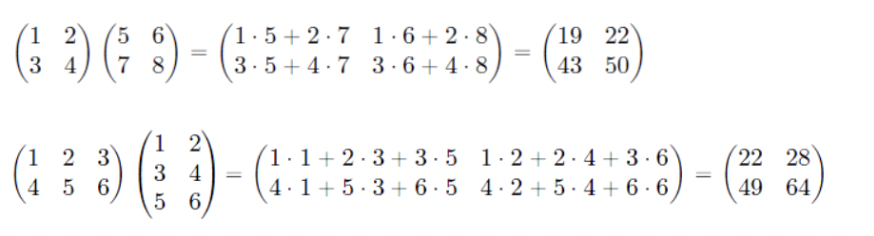
- m x n 행렬과 n x l행렬의 곱은 m x l 행렬이 된다.
- 행렬 곱은 numpy에서 np.dot()을 이용하여 구할 수 있다.
ex)

2. 신경망에서의 행렬 곱
- 신경망과 행렬곱은 무슨 연관이 있을까?
- 다음과 같이 신경망이 주어져 있다고 생각해보자

- 이를 식으로 나타내면 다음과 같은 식이 유도될 것이다.

- 이를 행렬 곱으로 나타내면 다음과 같아진다.
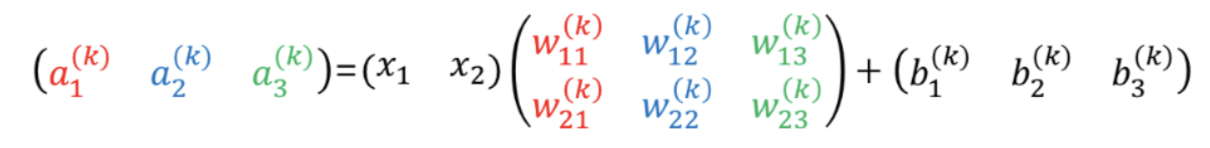
- 이에 관한 내용을 3층 신경망에 대해 빗대어 살펴보자.
3. 3층 신경망 구현하기
3.1. 3층 신경망 구조

- 이번에 구현하게 될 3층신경망을 설명해보자
- 입력층 (0층) : 2개
- 첫 번째 은닉층(1층) : 3개
- 두 번째 은닉층(2층) : 2개
- 출력층 (3층) : 2개
의 뉴런으로 이루어져 있다. 더 자세한 구조는 점차 알아가보자
3.2. 입력층 -> 1층 구현하기

- 이를 행렬곱으로 나타내면 다음과 같다.
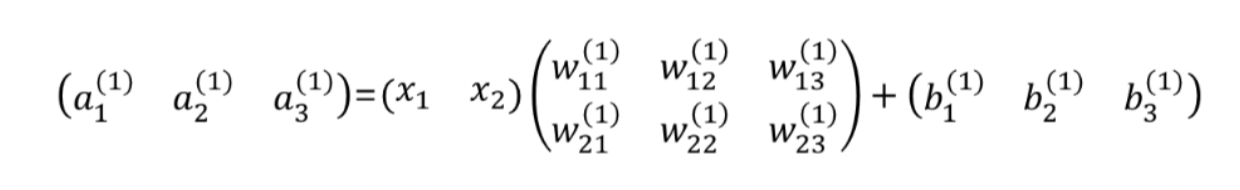
- (z1, z2, z3) = (h(a1) , h(a2), h(a3)) 가 된다. 이를 코드로 구현해보자.(Activation Function는 ReLU라고하자)
Code
X = np.array([1,2])
W1 = np.array([0.1,-0.2,0.3,-0.4,0.5,-0.6]).reshape(2,-1)
b1 = np.zeros(3)
A1 = np.dot(X,W1) + b1
Z1 = ReLU(A1)
Z1
#array([0. , 0.8, 0. ])
3.3. 1층 -> 2층 구현하기

- 이를 행렬곱으로 나타내면 다음과 같다.
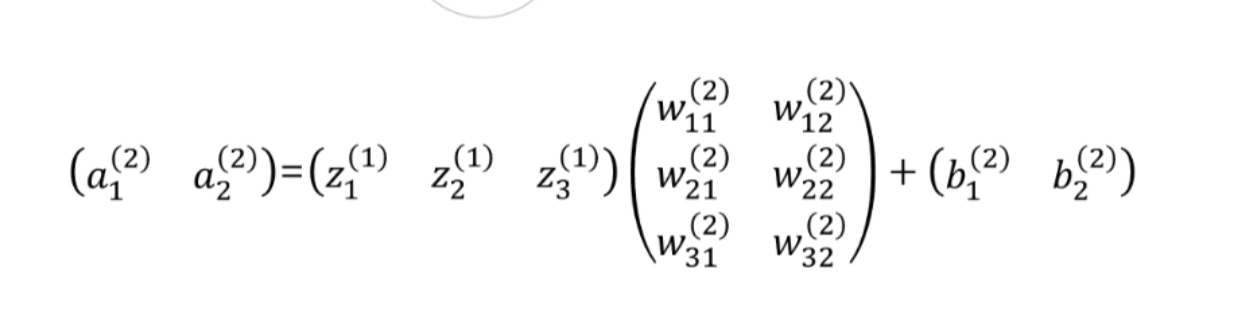
- 이를 코드로 구현해보자.
W2 = np.array([-1,2,3,4,5,-6]).reshape(-1,2)
b2 = np.ones(2)
A2 = np.dot(Z1,W2) + b2
Z2 = ReLU(A2)
Z2 # array([3.4, 4.2])
3.4. 2층 -> 출력층 구현

- 은닉층 -> 출력층의 특징은 마지막에 softmax 함수를 지난다는 것이다.
- SoftMax함수는 이따가 알아보도록 하고 이를 행렬곱으로 나타내면 다음과 같다.
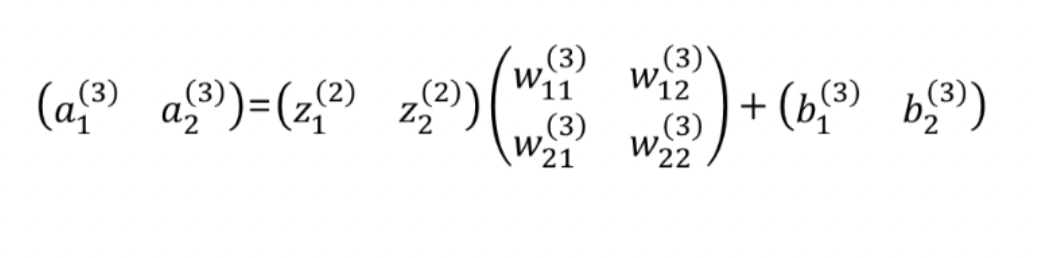
- 코드로 나타내면 다음과 같다.
def softmax(x):
return np.e**x/sum(np.e**x)
W3 = np.array([3,-4,3,-4]).reshape(2,2)
b2 = np.array([1,3])
A3 = np.dot(Z2,W3)+b2
Y = softmax(A3)
Y #array([1.0000000e+00, 5.8092829e-23])
3.5. 구현 정리
- 지금까지 나타낸 던 코드들을 한번에 정리하면 다음과 같다.
def init_network():
network = {}
network['W1'] = np.array([0.1,-0.2,0.3,-0.4,0.5,-0.6]).reshape(2,-1)
network['b1'] = np.zeros(3)
network['W2'] = np.array([-1,2,3,4,5,-6]).reshape(-1,2)
network['b2'] = np.ones(2)
network['W3'] = np.array([3,-4,3,-4]).reshape(2,2)
network['b3'] = np.array([1,3])
return network
def forward(network, x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x,W1) + b1
z1 = ReLU(a1)
a2 = np.dot(z1,W2) + b2
z2 = ReLU(a2)
a3 = np.dot(z2,W3) + b3
y = softmax(a3)
return y
network = init_network()
x = np.array([1,2])
y = forward(network, x)
y
-----------------------------------------------------------------------
#Output
array([1.0000000e+00, 5.8092829e-23])- 여기서 신경망을 dictionary로 저장한 이유는 해시맵 특성상 더 빠른 속도로 불러오는게 가능하기 때문이다.
4.SoftMax
- 앞서서 우리는 마지막 은닉층 -> 출력층으로 갈때 softmax 함수를 이용했었다.
- 이 softmax에 대해서 한번 알아가보자.

- 다음과 같이 exp()를 적용하고 normalize 해줘서 확률벡터로 나타나게 해주는 역할을 하게된다.
4.1. SoftMax 주의점
- softmax를 컴퓨터로 구현할 때 중요한 점은 OverFlow를 방지해줘야 한다는 것이다.
- 기본적으로 exp()를 사용하게 되는데 이는 너무 큰값을 뱉는다는 단점이 있다. -> OverFlow 발생
- 그래서 데이터의 최댓값을 모든 원소마다 빼주고 SoftMax를 진행해주면 된다.
- 이게 가능한 이유는 Softmax의 특징에서 알 수 있다.

- 해당 수식을 직접 SoftMax하게 되면 기존의 (x1,x2,x3)를 softmax한것과 결과값이 같아진다.
- 즉, C = -max(X) 일때도 같은값이 유도된다는 것이다.
- 그래서 컴퓨터에서 OverFlow가 일어나지 않게 코드를 작성하면 다음과 같다
def softmax(x):
x -= max(x)
return np.e**x/sum(np.e**x)
'DS Study > 밑바닥부터 시작하는 딥러닝 1' 카테고리의 다른 글
| [밑시딥1] [5] 손실함수(Loss Function) (0) | 2024.07.29 |
|---|---|
| [밑시딥1] [4] MNIST (0) | 2024.07.29 |
| [밑시딥1] [2] 활성화함수 (Activation Function) (0) | 2024.07.26 |
| [밑시딥1] [1] 퍼셉트론 (Perceptron) (0) | 2024.07.24 |

