0. Reference
https://arxiv.org/abs/1409.3215
Sequence to Sequence Learning with Neural Networks
Deep Neural Networks (DNNs) are powerful models that have achieved excellent performance on difficult learning tasks. Although DNNs work well whenever large labeled training sets are available, they cannot be used to map sequences to sequences. In this pap
arxiv.org
1. Introduction
- DNN은 음성 인식, Object Detection등 어려운 문제에서 뛰어난 성능을 발휘한다.
- 하지만 이러한 DNN도 한가지 중요한 한계가 존재한다.
- 그 한계는 입력과 출력이 고정된 차원의 벡터로 인코딩될 수 있어야 한다는 점이다.
- 즉, Sequence Data를 처리할 때 걸림돌이 된다는 것이다.
- 예를 들어, question answering 문제를 해결할 때,
- 질문을 나타내는 Sequence를 받고 답변을 나태내는 Sequence로 출력하는 과정으로 볼 수 있다.
- 하지만, 입출력의 차원이 사전에 고정될 수 없다는 점이 DNN에서의 큰 도전과제로 다가오게 된다.
- 본 논문에서 LSTM를 사용하여 Seq2Seq 문제를 해결하는 방법을 제안한다.
- 아이디어는 다음과 같다.
i) 첫 번째 LSTM : 입력 sequence를 한 time step씩 읽어들이거, 이를 고정된 크기의 벡터 표현으로 변환한다.
ii) 두 번째 LSTM : 이 벡터 표현을 기반으로 출력 시퀀스를 생성한다.

- 본 논문이 나오기 전의 연구에선 긴 문장을 다룰 때 LSTM 모델의 성능이 저하되는 문제가 보고되었었다.
- 하지만, 본 연구에선 Sequence의 순서를 완전히 reverse하는 기법을 사용하여 이를 극복하였다고 한다.
- 즉, 입력 문장의 단어 순서만 반대로 변환하고, 출력 문장은 그대로 유지했다고 한다. (apple --> x , elppa --> x)
2. The model
- RNN은 Sequence data를 다루기 위해 설계된 신경망이다.
- 이는 기존의 feedforward neural network을 Sequence data 처리에 적합하도록 일반화한 모델이라고 할 수 있다.
- RNN은 주어진 입력 sequence (x1,x2,...,xt)에 대하여 출력 Sequence (y1,y2,...,yt)를 다음과 같은 방식으로 계산한다.

- 하지만 이러한 Input sequence, output sequence의 길이가 가변적이거나
- non-monotonic 관계를 가지는 경우 적용이 어렵다고 한다.
- 이를 LSTM으로 한계를 극복할 수 있는데,
- LSTM은 long-term dependency을 학습할 수 있는 능력을 갖춘 RNN이라고 생각하면 된다.
- 이를 이용하면 입출력의 길이가 가변적인 Sequence 문제를 해결 가능하다.
- LSTM의 목표는 조건부 확률을 추정하는 것이다.
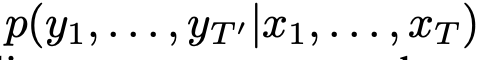
- LSTM은 다음과 같은 과정을 통해 이를 계산한다.
i) input sequence를 고정 크기의 벡터 v로 변환한다.
- LSTM의 마지막 Hidden state를 이용하여 입력 Sequence을 요약한 벡터를 생성한다.
ii) 이 벡터를 초기 상태로 설정하여 출력 Sequnce를 생성한다.
- 출력 확률을 LSTM-LM을 이용해 계산한다.

- 각 p(yt | v,y1,...,yt-1)는 softmax function을 통해 표현되며, vocabulary의 모든 단어에 대해 확률 분포를 형성한다
- 학습하는 과정에서 모든 문장은 특별한 EOS(End-of-Sentence)로 끝나야 한다.
- 이로 인해 모델이 다양한 길이의 Sequence를 학습할 수 있게 된다.
- 본 연구에선 Vanilla LSTM을 개선하기 위해 세 가지를 변형하였다고 한다.
i) 입출력을 위한 두 개의 LSTM 사용
-- 하나의 LSTM이 입력 sequence를 처리하고, 다른 하나가 출력 sequence를 생성한다.
-- 이는 모델의 파라미터 수를 증가시키면서도 계산 비용을 거의 늘리지 않는다고 한다.
-- 여러 언어 쌍을 동시에 학습하는 데 용이하다고 한다.
ii) Deep LSTM사용
-- shallow LSTM보다 Deep LSTM이 훨씬 높은 성능을 보였다고 한다.
-- 본 연구에선 4개의 Layer의 LSTM을 사용하였다고 한다.
iii) 입력 Sequence를 Reverse하기
이러한 3가지 변형으로 인해 Vanilla LSTM에 비해 더 성능이 향상되었다고 한다.
3. Experiments
- 본 연구에서는 WMT'14 영어-프랑스어 기계번역을 목적으로 실험을 진행하였다.
3.1. Dataset details
- 본 연구에서 사용하게 된 Dataset은 WMT'14 English to French dataset이다.
- WMT'14 English to French dataset같은 경우 많은 NLP에서 사용이 되는 dataset이므로 기억해두면 좋다.
- 만일 Vocaburaly에 없는 단어라면 "UNK"라는 토큰으로 대체하였다고 한다.
3.2. Decoding and Rescoring
- 훈련 목표는 주어진 입력 문장 S에 대하여 올바른 번역 T의 log probability를 Maximizing하는 것이다.

- 훈련이 완료된 후, 다음 식을 통해 가장 확률이 높은 번역을 선택하게 된다.

- Beam Search Decoding을 적용하였다고 한다.
- Beam Search을 알아보기 전에, Greedy Decoding에 대해서 먼저 알고 넘어가보자.
- Greedy Decoding은 다음과 같이 해당 시점에서 가장 확률이 높은 후보를 선택하는 것이다.
- Time Complexity면에선 훌륭한 방법이지만, 최종적인 결과물의 정확도 관점에선 그렇게 좋은 모습을 보이진 않는다.
- 이러한 예측과정에서 한번이라도 틀리게 된다면 그 뒤부터 완전히 망가져버리게 된다.

- 이러한 Greedy Decoding의 단점을 극복하기 위해 나오게된 기법이 Beam Search Decoding이다.
- 이웃한 k개의 단어를 골라 가장 확률이 높은 것을 선택하는 기법이다.

- 본 논문에선 beam size가 1이여도 우수한 성능을 보였다고하지만, beam size가 2인 경우 더 좋은 성능을 이끌었다고 한다.
cf) beam size == 1이면, greedy decoding과 똑같음
3.3. Reversing the Source Sentences
- LSTM은 Long-term dependencies를 처리할 수 있으나,
- 입력 문장을 reverse로 변환하니까 학습 성능이 크게 향상되었다고 한다.
- 그 이유는 다음과 같다고 한다.
- 원래 문장 구조에선 input 단어와 output 단어 사이의 거리가 크다고 한다. (그래서 최적화가 어려움)
ex)
- a->p->p->l->e-> EOS (a와 EOS사이의 거리가 4)
- e -> l -> p -> p -> a -> EOS (a와 EOS사이의 거리가 0)
- 이렇게 입력을 reverse로 변환하면 초기 단어 간의 short-term dependency가 증가한다고한다.
4. Conclusion

- 거의 SOTA급의 결과를 이끌었다는 것을 알 수 있다.
- 즉, 딥러닝 기반 번역 시스템이 실용적인 수준으로 발전헀음을 보여주는 중요한 성과로 볼 수 있는 것이다.
'Paper Review(논문 리뷰) > Deep Learning' 카테고리의 다른 글
| [논문 리뷰] [DL] When Does Label Smoothing Help? (0) | 2025.03.20 |
|---|---|
| [논문 리뷰] [Deep Learning] Memory Networks (0) | 2025.02.07 |
| [논문 리뷰] [Deep Learning] empirical evaluation of gated recurrent neural networks on sequence modeling (0) | 2025.02.05 |
| [논문 리뷰] [Deep Learning] LSTM: A Search Space Odyssey (1) | 2025.02.05 |
| [논문 리뷰] [Deep Learning] Long Short-Term Memory (1) | 2025.02.04 |
