1. Introduction
- Lecture 14부터 Unsupervised Learning에 대해서 알아갈 것이다.
- 즉, unlabeled data를 이용하여 학습하는 것을 의미한다.
2. K-means Clustering
- Clustring이란 말 그대로 군집화하는 걸 의미하는데,
- labeling되어있지 않는 데이터를 다음과 같이 군집화 하는 것을 의미한다.
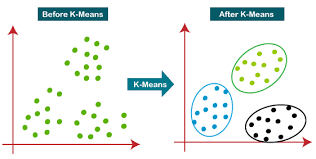
- K-means Clustering의 과정은 다음과 같다.

- 이를 보기 좋게 시각화해서 보이면 다음과 같이 행동하게 된다.

- k-means clustering을 수식으로 나타내면 다음과 같다.
- 만일 training set이 {x_1,x_2,...,x_n}으로 주어져 있다고 해보자.
- 우선 각 cluster의 center를 initialization해야한다.
- 이를 무작위로 다음과 같이 설정한다고 해보자.
- 여기서 k는 군집화 하게 될 개수를 의미한다.( 위 그림에선 k = 5)
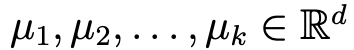
- 다음 과정을 수렴할 때 까지 계속 반복하면 된다.
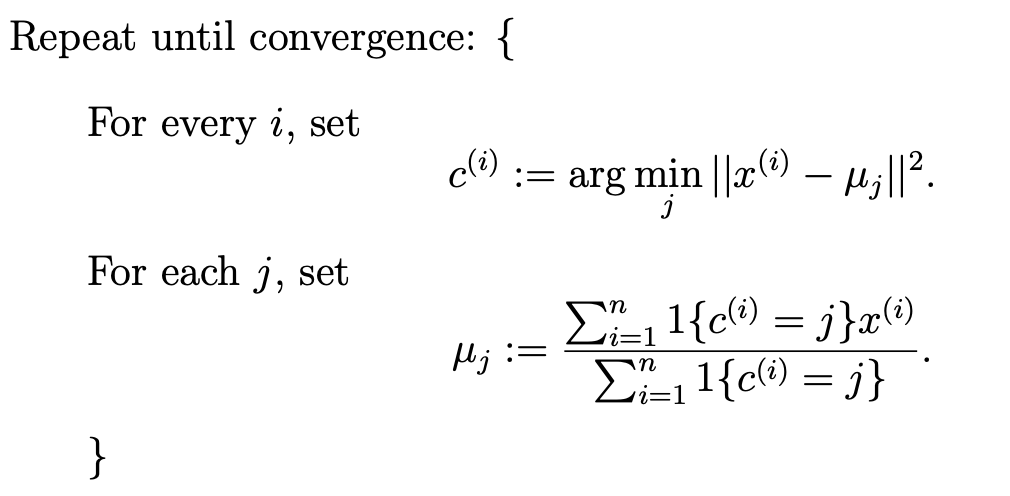
- Repeat되는 부분이 총 두 단계로 이루어 진것을 확인할 수 있는데,
- 첫 번째 단계는 cluster의 center와 거리가 가까운 점을 같은 색으로 칠하는 것이다.
- 두 번째 단계는 cluster의 center를 같은 색으로 칠한 점들과 거리의 차이가 줄어드는 방향으로 update하는 것을 의미한다.
- 즉, 두 번째 단계는 군집화 했던 데이터의 평균을 의미한다.
2.1. cost function
- K-means Clustering의 cost function은 다음과 같이 정의된다. (무조건 수렴한다고 알려져있다.)

- K의 크기는 어떻게 잡아야 하는 걸까?
- 이는, 개발자의 목적에 따라 달라지므로 수동으로 선택해야한다고 주장하고 있다.
- 어떤 학생이 다음과 같은 질문을 하였다.
"만일 local minima에 빠지면 어떻게 해야하냐?"
- 해당 질문에 10번,100번 전부 랜덤한 position에 돌려서 가장 최적의 값을 도출하면 된다라고 말을 한다.
3. Anomaly Detection

- x로 표시되어 있는 point cloud들은 어떤 특정 기계를 feature에 따라 분포를 나타낸 것인데,
- 이때 오른쪽 위 초록색 점은 누가봐도 이상이 있다는 걸 인지 할 수 있다.
- 이때 model을 p라고 하면, p(x) < threshold 보다 작다면, 이상이 있다고 말할 수 있을 것이다.
- 그러면 이걸 어떻게 modeling할 수 있을까?
- 간단히 생각해서, 왼쪽위의 데이터의 분포와 오른쪽 아래의 데이터의 분포를 동시에 생각해주면 된다.
4. Mixture of Gaussians Volatile
- 조금 더 단순하게 생각하기 위해서 x 데이터가 전부 1차원이라고 생각해보자.

- unsupervised learning이기 때문에 unlabeled data라고 할 수 있다.
- 데이터의 modeling을 위해 다음과 같은 joint distribution을 정의해보자.

- 여기서 z는 multinomial distribution에 속한다.
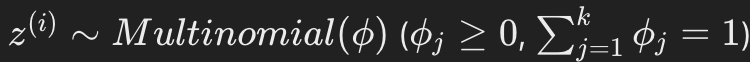
- phi = p(z=j)

- 이런 model을 GMM(Gaussians Mixture Model)이라고 불린다.
- 여기서 z는 latent variable이다. (이는 아직 드러나지 않은 특징을 의미한다.)
- 이에 따른 likelihood를 써보면 다음과 같은 식이 나온다.
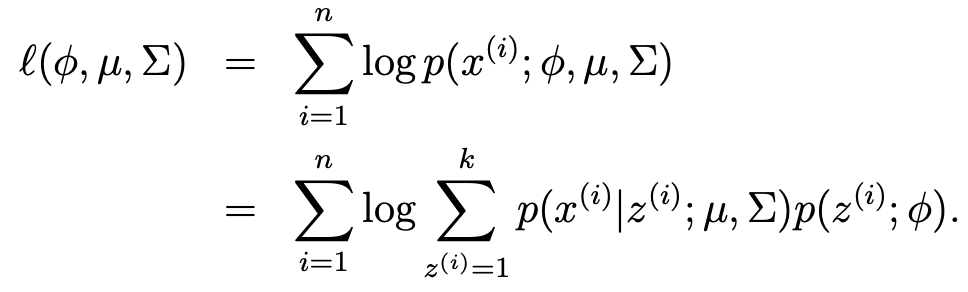
- 해당 식은 미분하기 쉽지 않기 때문에, maximization되는 parameter는 다음과 같이 약속되어있다.

5. Expectation Maximization Algorithms
- EM Algorithms은 iterative algorithm으로 두 가지 주요 단계로 주어진다.
i) E-Step
- Model이 z의 값을 추측하는 단계이다.
ii) M-step
- 이러한 추측을 바탕으로 모델의 parameter를 update한다.
- 조금 더 자세히 알아보자면,
i) E-Step
- 각 i,j에 대해 w를 설정한다.(분포를 추측하는 단계이다.)

ii) M-step
- 위의 추측한 분포에 맞춰 parameter를 update해준다.
- MLE를 찾는 과정이라고 생각하면 된다.

- 조금 더 이해하기 쉽게 밑의 글에 나온 그림을 참고하여 나타내면 다음과 같다.
https://angeloyeo.github.io/2021/02/08/GMM_and_EM.html#google_vignette
GMM과 EM 알고리즘 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io


6. Jensen's Inequality
- Jensen's Inequality는 convex function에 적용된다.
- 정의는 다음과 같다.
" 함수 f의 정의역이 실수 집합이고, f가 convex하다고 가정하자. 모든 x에 대하여 f''(x) >= 0 을 만족하게 된다."

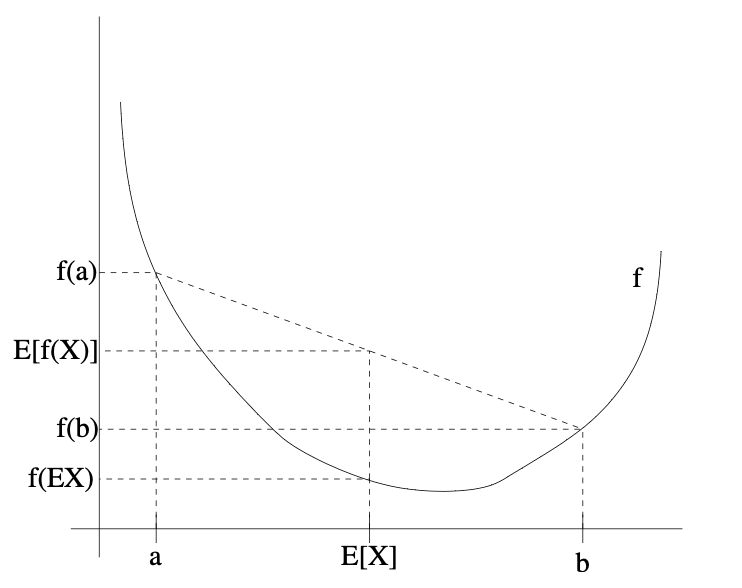
- 젠센의 부등식은 lecture 15에서 활용하게 된다.
'DS Study > CS 229(Machine Learning)' 카테고리의 다른 글
| [CS 229] [15.5] Lecture 15.5 - PCA(principal Component Analysis) (0) | 2025.02.09 |
|---|---|
| [CS229] [15] Lecture 15 - EM Algorithm & Factor Analysis (0) | 2025.02.09 |
| [CS229] [13] Lecture 13 - Debugging ML Models and Error Analysis (0) | 2025.02.08 |
| [CS229] [12] Lecture 12 - Backprop & Improving Neural Networks (1) | 2025.02.07 |
| [CS229] [11] Lecture 11 - Introduction to Neural Networks (0) | 2025.02.07 |
