1. EM Algorithms
- 다음과 같이 m개의 training dataset이 있다고 가정해보자.
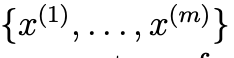
- 우리의 목표는 데이터에 맞추어 모델 p(x,z)의 parameter를 추정하는 것이다.
- 이때 likelihood는 다음과 같이 정의된다.

- 여기서 z는 latent variable이다.(latent variable은 표현되지 않은 잠재적 feature라고 생각하면 된다.)
- Expectation-Maximization algorithms을 통해 MLE을 효율적으로 계산할 수 있다.
- l(theta)을 직접적으로 극대화하는 것은 어렵기 때문에,
- lower-bound을 반복적으로 구성한 후(E-step)
- (M-step) 해당 lower-bound을 최적화하는 전략을 사용하게 된다.
- 각 i에 대해, Q_i를 z에 대한 어떤 분포라고 하자. 그러면 다음과 같은 식이 유도가 된다.

- 여기서 (3) Step은 Jensen의 부등식을 사용하여 유도된 것이다.
- f(x) = log x는 concave function이기 때문에 Jensen 부등식을 적용할 수 있다.
- 위의 식에서 lower-bound가 특정한 theta에 대해 타이트하게 유지되도록 Q_i를 선택하게 된다.
- 즉, 부등식이 equality가 되도록 만들어 준다는 의미이다.
- 이를 위해 Q_i는 다음과 같이 설정된다.


- 즉, E-step에선 Q_i를 데이터 x와 현재의 theta에 대해 z의 posterior probability로 설정되게 된다.
- 그 후, M-step에서 다음과 같은 식을 최저화하여 새로운 theta 값을 얻는다.

- 다시 EM-algorithms을 정리하면 다음과 같다.
1) E-step : Qi(z) = p(z|x;theta)로 설정
2) M-step : theta를 위의 objective fuction을 maximization하는 값으로 update
3) 수렴할 때 까지 반복
2. Mixture of Gaussians revisited
- EM algorithms을 바탕으로 GMM의 paramter들을 추정하는 예제로 돌아가보자.
- 해당 포스팅에선 phi,mu만 M-step update를 다룰것이다.
2.1. E-step
- E-step은 간단하다.
- 위에서 유도한 알고리즘에 따라 다음을 계산하면 된다.

- 여기서 Q_i는 분포 Q_i에 따라 z가 값 j를 가질 확률을 나타낸다.
2.2. M-step
- M-step에선 다음을 Maximization해야한다.

- 그렇기 때문에, mu와 phi에 대해 update는 다음과 같이 이루어 진다.


- phi는 다음과 같이 유도할 수 있다.
- phi와 관련된 항만 그룹화 하면 다음과 같다.
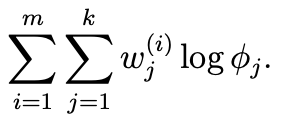
- phi는 확률이기 때문에 다음을 제약조건을 갖는다.

- 라그랑주 승수법을 통해 해결해보자.

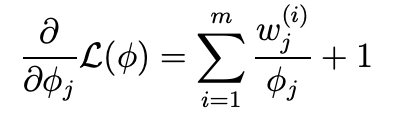

3. Factor Analysis
- x 가 n차원의 데이터라고 가정해보자.
- 이 데이터가 여러개의 GMM으로 부터 생성되었다면, EM Algorithms을 통해 혼합 모델을 적용시킬 수 있다.
- 일반적으로 충분한 데이터를 가지고 있다고 가정하여, 이를 통해 데이터 내 여러 Gaussians Structure를 구별할 수 있다.
- 이는, train data의 크기(m)가 data의 dimension보다 훨 씬 클 때 이러한 조건이 성립된다.
- 만약 n >> m인 상황이면 어떨까?
- 이러한 문제에서 single Gaussians으로 데이터를 설명하는 것 조차 어려울 것이며, GMM을 사용하는 것은 더 어려울 것이다.
- 자세히 설명하자면, m개의 데이터가 R^n의 subspace에 속하기 때문에,
- data를 Gaussians distribution으로 모델링하여 MLE로 평균과 공분산을 계산하면 다음과 같다.

- 하지만 해당 공분산은 singular하기 때문에, 역행렬이 존재하지 않는다.
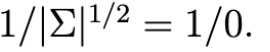
- 하지만, 두 값은 multivariate Gaussians Distribution의 density를 계산하는 데 필요하다.
- 이 문제를 다르게 표현하자면, MLE의 결과는 데이터를 포함한 affine space에 모든 확률을 배치하는 Gaussians을 생성하며,
- 이는 Singlar Covariance matrix에 해당되게 된다.
- 즉, 일반적으로 m >> n을 만족하지 않는다면, 평균 밀 공분산의 MLE는 매우 부정확할 가능성이 높아진다.
- 그럼에도 불구하고, 데이터를 잘 설명할 수 있는 합리적인 Gaussians model을 적용하고 싶고,
- 데이터 내 Covariance 을 찾고 싶다면 어떻게 해야할까?
3.1. Restrictions of Covariance Matrix
- 데이터가 부족하여 완전한 coviarance matrix을 fit할 수 없을 때, Covariance matrix에 제약을 가하는 방법을 고려할 수 있다.
i) Diagonal matrix covariance matrix
- covariance matrix을 Diagonal matrix로 가정한다. 이 경우, MLE는 다음과 같다.
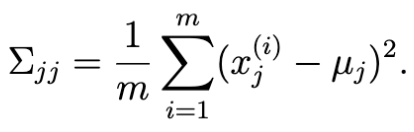
ii) 모든 대각원소 값이 동일한 Covariance Matrix
- 대각 원소의 모든 값이 동일하게 설정할 수도 있다.
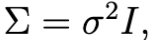
- 이 때, MLE는 다음과 같다.

- 하지만 이러한 제약에도 특정 상황에서는 데이터 간의 correlation을 설명하지 못할 수 있다.
3.2. Marginals and conditionals of Gaussians
- factor analysis을 설명하기 전에, joint multivariate Gaussians Distribution을 가지는
- random variable의 conditional and marginal distribution을 구하는 방법에 대해서 알아보자.
- random variable x가 다음과 같이 주어진다고 가정해보자.

- 주어진 조건에서 x1과 x2는 joint multivariate Gaussians Distribution을 가진다.
- x1의 marginal distribution은 다음과 같다.

- 여기서 E[x1] = mu_1 , Cov(x_1) = sigma_11이다.
- 여기서 공분산 정의는 다음과 같은데,
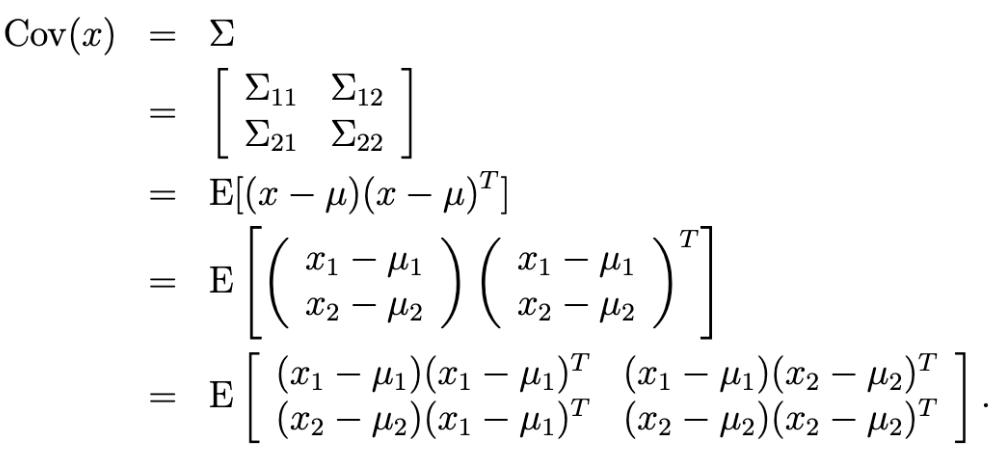
- 마지막 결과의 좌상단 block matrix을 의미한다.
- x2가 주어졌을 때, x1의 conditional distribution은 다음과 같이 정의된다.


- 해당 식들은 전부 factor analysis에서 유용하게 사용될것이니, 잘 기억해보자.
3.3. The factor Analysis model
- factor analysis model에선 (x,z)의 joint distribution을 다음과 같이 정의한다.( z는 k차원의 latent variable)

- 여기서 각 parameter들은 다음과 같이 정의된다.

- 데이터 생성 과정에 대해 알아보자.
- 각 데이터 point x_i는 다음 단계를 통해 생성된다고 할 수 있다.
i) k차원의 multivariate Gaussians z ~ N(0,1)을 sampling한다,.
ii) z를 통해 mu + lambdaz를 계산하여 R^n의 k차원 affine space에 mapping한다.
iii) 여기에 covaraince matrix psi의 nosie를 추가하여 x를 생성한다.
- 즉, 식으로 정리하면 다음과 같다.
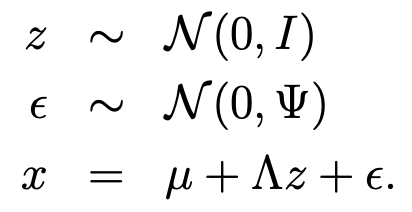
- 이제 이 모델이 정의하는 distribution을 정확히 분석해보자.
- random variable z와 x는 다음과 같은 joint Gaussians distribution을 갖는다.

- 그후 각 평균과 공분산을 구해보면 다음과 같다.
- E[z] = 0 이다. (z ~ N(0,1))

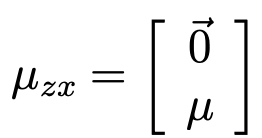
- covariance matrix는 다음과 같이 계산된다.

- 종합적으로 확인하면 다음과 같다.

- marginal distribution에 대해서 한번 구해보자.
- marginal distribution x는 다음과 같이 주어진다.
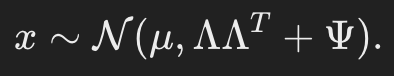
- 이에 따른 log likelihood는 다음과 같다.

- 해당 log likelihood를 통해 MLE를 구해야 하는데 평범한 방법으로 구하기 힘들다.
- 그래서 EM Algorithms을 통해 구하게 된다.
3.4. EM for factor analysis
- E-step은 다음과 같다.
- 우선 우리는 다음을 계산해야 한다.

- 밑에 있는 두 식에 [x,z]에 대한distribution을 대입해보자.
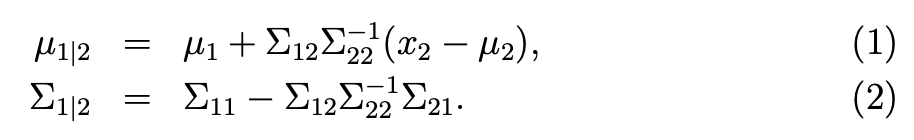

- 이 평균과 공분산을 다시 Q에 대해 대입하면 다음과 같은 결과를 도출할수있다.

- 이제 M-step을 가보자.
- 최적화해야하는 것은 다음과 같다. (z가 이산적이지 않고 연속적이기에 적분으로 들어간다.)

- 여기선 lambda에 대해서만 최적화한다.
- 위의 식을 다음과 같이 단순화할 수 있다.(로그안에 곱형태를 합차형태로 분리해준것이다.)

- 이를 Expectation형태로 표현하면 다음과 같다.

- 여기서 parameter에 영향을 받지 않는 항을 제거하면 다음과 같은데, 이를 maximization해야한다.

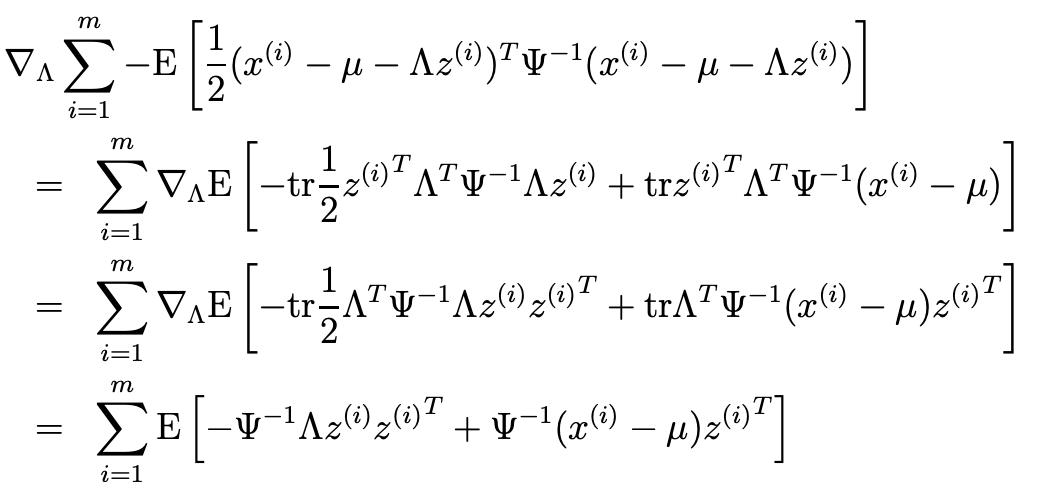
- 이거 자체를 0이라 두고 lambda를 찾으면 다음과 같다.
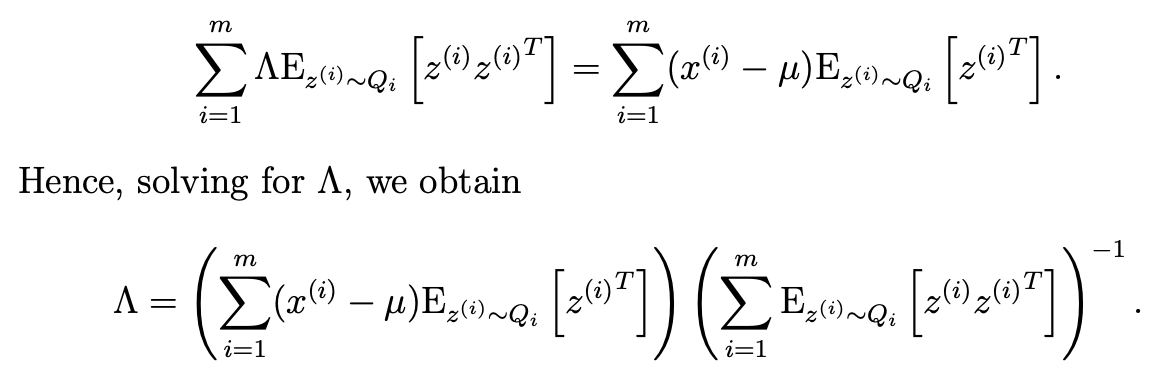
- 나머지 파라미터들은 다음과 같다.
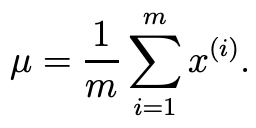
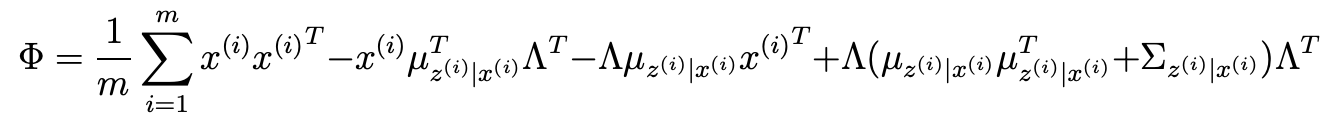
'DS Study > CS 229(Machine Learning)' 카테고리의 다른 글
| [CS229] [16] Lecture 16 - Independent Component Analysis & RL (2) | 2025.02.09 |
|---|---|
| [CS 229] [15.5] Lecture 15.5 - PCA(principal Component Analysis) (0) | 2025.02.09 |
| [CS229] [14] Lecture 14 - Expectation-Maximization Algorithms (2) | 2025.02.08 |
| [CS229] [13] Lecture 13 - Debugging ML Models and Error Analysis (0) | 2025.02.08 |
| [CS229] [12] Lecture 12 - Backprop & Improving Neural Networks (1) | 2025.02.07 |
