1. Reinforcement Learning
- RL은 간단하게, 모든 Step에서 올바른 답을 말하라고 요구하지 않는 알고리즘이다.
- 우리같은 엔지니어들이 할 일은 모델이 잘 할떄와 못할 때를 알려주는 reward function를 지정해줘야 한다.
- 즉, 모델이 일을 잘 동작할 때마다 높은 reward를 주는 reward function을 작성해야 하고,
- 반대면 낮은 reward를 주는 reward function을 작성해야한다.
- 만일 체스 ai를 만든다고 생각해보자, 이 ai가 만약 50수에서 져서, -1 이라는 reward를 받는다고 생각해보자.
- 근데, ai가 지게 된 요인이 49수일까? 30수때부터 잘못둬서 뒷 일이 전부 꼬일 수 도 있다.
- 즉, 어떤 순간부터 불리하게 작용하였는지를 알아야 적절한 reward를 취해줄 수 있다는 것이다.
- 이를 Credit assignment problem이라고 한다.
1.1. MDP(Markov Decision Process)
- Reinforcement Learning은 보통 MDP로 문제를 해결해나간다고 한다.
- 그럼 MDP는 무엇일까?
- MDP는 5개의 tuple로 이루어져 있다.
i) S : set of State (ex, 모든 가능한 체스 위치의 집합, 헬리콥터의 조정 가능한 위치의 집합..)
ii) A : set of actions (ex, 체스 게임에서 할 수 있는 모든 움직임의 집합..)
iii) {P_sa} : state transition probabilities(특정 행동 a와 특정 상태 s를 취할 때,특정 다른 상태의 최적 상태에 도달할 확률)
iv) gamma : discount factor [0,1)
v) R : Reward function
- MDP의 동작은 다음과 같이 진행된다.
i) 초기 상태 s_0에서 시작한다.
ii) 상태 s_0에서 a_0 ㅌ A 라는 행동을 선택한다.
iii) 이 행동의 결과로 MDP는 P_(s_0a_0)에 따라 무작위로 다음 상태 s_1로 전이된다.
iv) 이후, 상태 s_1에서 새로운 행동 a_1 ㅌ A를 선택한다. 이를 계속 반복한다.
- 이를 도식화 하면 다음과 같다.
- MDP에서 payoff는 다음과 같이 계산된다.(마치 이자와 비슷한 느낌)
- 이러한 discount factor는 결국 payoff가 수렴하도록 만들어주는 역할을 하게 된다.
- RL의 목적은 해당하는 payoff의 Expectation을 Maximization하는 행동을 step에 따라 선택하는 것이다.
- 대부분의 RL에서는 state -> action으로 mapping 시키는 policy를 정의한다. (ex, 날씨가 흐림(s) --> 우산을 챙김(a))
- 이러한 policy는 얼마나 있을까?
- 만일 가능한 state가 11개고, action이 4개라고하면 총 policy는 4^11개가 될 것이다.
- 즉, state가 s개고 action이 a개면 가능한 policy는 a^s개가 된다.
- 그러면 가장 좋은 policy를 선택하려면 어떻게 해야할까?
- 최적의 policy를 구하려면, 세가지를 정의해야한다.
i) V^ㅠ : (policy ㅠ에 대한 value function)
- policy ㅠ 에 대하여, V^ㅠ는 S -> R로 mapping하는 함수이다.

- 해당 value function을 재귀적으로 다시 적으면 다음과 같이 수정 가능하다.

- 여기서 s' ~ P_sㅠ(s) 를 뛴다. a = ㅠ(s)이기 때문에, 다음과 같은 식이 유도가 된다.

- 해당 벨만 방정식은 V^ㅠ를 효율적으로 계산하는 데 사용 가능하다.
- 특히, 공간이 유한한 MDP에서는 이를 |S|개의 선형 방정식을 |S|개의 미지수(V^ㅠ(s))에 대해 풀어야 하는 문제가 된다.
- 즉, 해당 Linear Equation을 풀어서 V^ㅠ(s)값을 효율적으로 계산할 수 있게 된다.
- 여기서 우리는 Optimal value function을 정의할 수 있는데, V^ㅠ의 max값으로 정의 된다.

- Optimal value function은 모든 가능한 policy중에서 기대되는 할인된 보상의 총합이 최대가 되는 값을 의미한다.
- Optimal value function에 대해 Bellman Equation로 나타내보자.

- 현재 상태에서 가능한 모든 행동 a에 대해, 가장 큰 미래 보상을 가져오는 행동을 선택하는 방식이라고 볼 수 있다.
- 이번에 Optimal policy를 ㅠ^* 를 다음과 같이 정의한다.

- Optimal policy는 Optimal value function를 최대화하는 행동 a를 선택하는 policy이다.
- 모든 상태 s와 모든 정책 ㅠ에 대해 다음 관계가 성립한다.
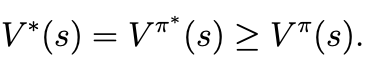
- 첫 번째 등식은 Optimal policy ㅠ^* 를 따를 때의. value function V^(ㅠ^*)(s)가 Optimal value function V^*(s)
- 부등식은 어떤 policy ㅠ를 선택하더라도, 그 policy의 value function가 optimal policy의 value function보다 클 수 없음을 의미한다.
2. Value iteration and policy iteration
- MDP을 해결하기 위한 두 가지 알고리즘을 설명한다.
2.1. Value Iteration
- 첫 번째 알고리즘인 value iteration은 다음과 같이 진행된다.
1) 각 상태 s에 대해 초기값를 설정한다.
--> V(s) := 0
2) 수렴할 때 까지 반복:

- 해당 알고리즘은 벨만 방정식을 반복적으로 업데이트하여 추정된 Value function V(s)를 점진적으로 개선하는 방식으로 작동한다.
- 업데이트 과정은 두 가지 방식으로 수행될 수 있다.
1. 동기식 업데이트(Synchronous Updata)
-- 모든 상태 s에 대해 새로운 V(s) 값을 계산한 후, 한꺼번에 기존 값들을 새 값으로 덮어씀
-- 이 방식은 "Bellman Backup Operator"를 실행하는 것으로 볼 수 있다.
2. 비동기식 업데이트(Asynchronous Update)
-- 상태들을 순차적으로 반복하면서, 기존 값을 즉시 업데이트한다.
-- 특정 순서로 상태를 방문하며 갱신하는 방식
- 어떤 방식으로 업데이트하든 value iteration은 V^*로 수렴하게 된다고 한다.
- 이후 다음 식을 사용하여 Optimal Policy를 찾을 수 있다.

2.2. policy iteration
- value iteration과는 다르게 policy iteration은 optimal policy를 찾기 위한 또 다른 표준적인 알고리즘이다.
- policy iteration algorithms은 다음과 같다.

- Loop에선 현재 policy에 대한 value function V를 계산한 후, 그에 따라 policy를 업데이트하는 과정을 반복한다.
- (b)단계에서, policy를 업데이트를 할 때 현재 value function에 대해 greedy하게 policy를 선택하게 된다.
- (a)에서 V 계산은 벨만 방정식을 푸는 과정으로, |S| 개의 선형 방정식을 풀어내야한다.
- 이 과정을 몇 번 반복하면 V는 V^*로, ㅠ는 ㅠ^*로 수렴하게 된다고 한다.
3. Learning a model for an MDP
- 실제로 헬리콥터나, 로봇 개,체스 봇을 구현하기 위해 state transition probabilities를 미리 아는건 불가능에 가깝다.
- 많은 MDP에선 데이터를 이용하여 state transition probabilities를 추정하게 된다.
- 예를 들어 다음과 같이 여러번 실험을 진행했다고 가정해보자.
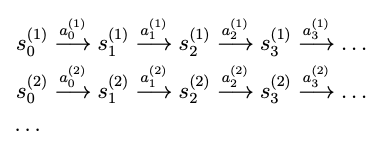
- 이러한 MDP 경험이 주어지면, 우리는 state transition probability를 MLE를 통해 다음과 같이 계산이 가능하다.

- 만약 한번도 실행하지 않았던 경우 0/0이 되는데 이를 1/|P_sa|로 초기화한다고 한다.
- Lapalce Smoothing을 이용해도 되지만, 강화학습에선 그렇게까지 신경을 쓰는 편은 아니라고 한다.
- MDP를 해결하기 위해 우리는 다음과 같이 구현하면 된다고 한다.

- 이를 통해 ㅠ^*를 얻어 낼 수 있다.
'DS Study > CS 229(Machine Learning)' 카테고리의 다른 글
| [CS229] [18] Lecture 18 - Continous State MDP & Model Simulation (0) | 2025.02.14 |
|---|---|
| [CS229] [16] Lecture 16 - Independent Component Analysis & RL (1) | 2025.02.09 |
| [CS 229] [15.5] Lecture 15.5 - PCA(principal Component Analysis) (0) | 2025.02.09 |
| [CS229] [15] Lecture 15 - EM Algorithm & Factor Analysis (0) | 2025.02.09 |
| [CS229] [14] Lecture 14 - Expectation-Maximization Algorithms (2) | 2025.02.08 |





