1. State Space
- Lecture 17에선 이산적인 MDP에 대해서 알아보았다면, 이번 lecture에선 연속적인 MDP에 대해서 다뤄본다고 한다.
- 우선 예를 들어 자율주행 자동차를 모델링한다고 가정해보자.
- 자동차의 state를 모델링하기위해서, (위도,경도)로 좌표를 나타낸다. 이를 (x,y)로 치환하자.
- 그리고 자동차가 어떤 방향으로 나아가는지 궁금할 것이다. 이를 가속도로 나타낸다. theta
- 만약 자동차의 속력이 달라진다면 이때 (x',y',theta')으로 정의해보자.
- 이제 자동차에 대해 모델링을 진행할 건데, 모델링은 엔지니어들마다 다를 것이다.
- 누군가는 타이어의 마모가 중요하다고 생각할 것이고, 누군가는 자동차의 엔진의 온도를 중요하다고 생각할 것이다.
- 즉, 모델링은 어디에 apply할것인지에 따라 달라지게 된다.
2. Discretizaiton
- 연속적인 state space를 다루는 가장 직접적인 방법은 연속적인 공간을 이산적인 공간으로 만드는 것일 것이다.
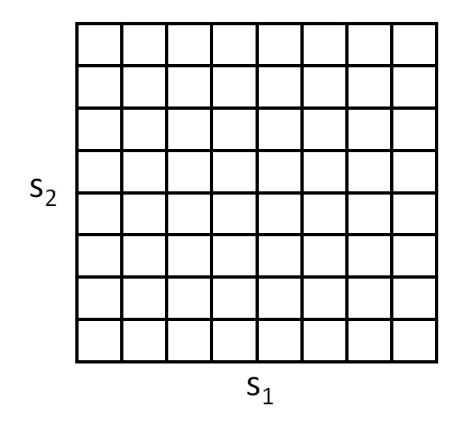
- 다음과 같이 s2,s1이라는 연속적인 state를 구간을 나눠서 이산적으로 만들어주면 된다.
- 한개의 사각형은 전부 같은 값을 가지게 된다.
- 이러한 이산화의 단점은 무엇일까?
- 첫 번째 단점은 V*나 ㅠ*를 계산할 때 너무 Naive하게 구해지게 된다는 것이다.
- 두 번째 단점은 curse of dimensionality를 갖게 된다는 것이다.
- S = R^n에 있고, 각 차원을 k 값으로 이산화하면, k^n개의 이산화한 공간을 얻게 된다.
- 즉, 차원이 커지면 커질수록 매우 많은 공간을 요구하게 된다는 것이다.
3. Guidelines
- 만일 S가 2,3차원이라면 그냥 이산화하면된다고 한다.
- 4~6차원이라도 그냥 이산화하면되는데, s1~s6까지 민감하게 반응하는 아이가 있다면, 그 부분은 세밀하게 쪼개면 된다.
- 7~ 부턴 이산화하지 않는게 좋다고 한다.
4. Value Function Approximation
- 이제 연속 MDP에서 policy를 찾는 대안적인 방법을 설명한다. 이 방식에는 V*을 직접 Approximation하여
- discretization을 사용한다. 이 접근법을 value function approximation이라고 불린다.
4.1. Using a model or simulatior
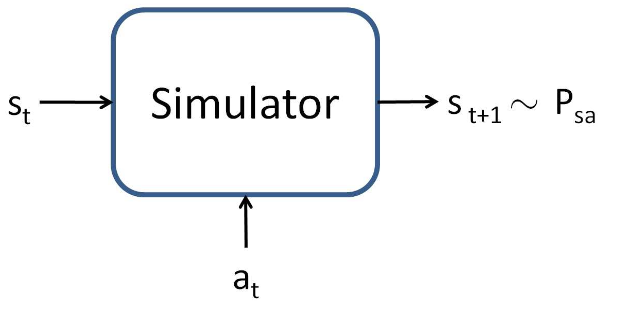
- value function approximation을 구현하기 위해, 우리는 MDP에 대한 model 혹은 simulator가 있다고 가정하자
- simulator는 black box 모델로서 어떤 연속적인 s_t와 a_t를 입력받아 다음 상태 s_t+1를 출력한다.
- 이 출력은 state transition probability P_stat에 따라 sampling된다.
- 모델을 구축하는 방법에는 여러 가지가 있다.
- 그 중 하나는 "physics simulation"을 사용하는 것이다.
- 또 다른 방법은 기성 물리 시뮬레이션 소프트웨어를 사용하는 것이다.
- "기계 시스템의 전체적 물리적 설명, s_t, a_t"를 입력으로 받아 짧은 시간 후의 상태 s_t+1를 계산한다.
- 또 다른 방법은 MDP에서 수집된 데이터로부터 모델을 학습하는 것이다.
- 예를 들어, "m번의 시뮬레이션"을 실행하고, 각 시뮬레이션에서 T번의 timesteps동안 MDP에서 행동을 수행한다고 가정하자.
- 이러한 실험은 random actions, policy실행, 또는 기타 다른 방식으로 실행될 수 있다.
- 이를 통해 다음과 같은 m개의 state sequence를 관찰 가능하다.
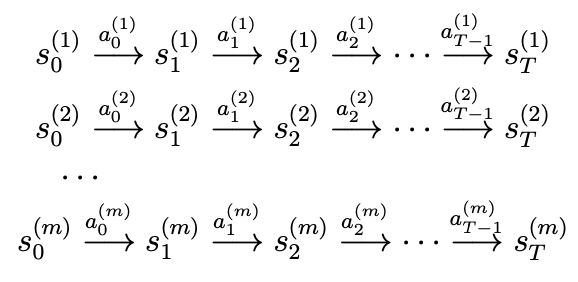
- 이제 학습 알고리즘을 사용하여 다음 상태 s_t+1를 s_t와 a_t의 함수로 예측하게 된다.
- 또 다른 방법은 linear model을 학습한다.
- 즉, 다음 상태를 아래와 같이 linear equation을 근사할 수 있다.
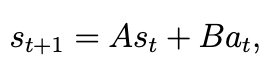
- 이는 lienar regression과 유사한 알고리즘을 사용하여 학습된다.
- 모델의 parameters는 행렬 A와 B이며, 실험에서 수집한 데이터부터 다음 최적화 문제를 풀어 추정할 수 있다.
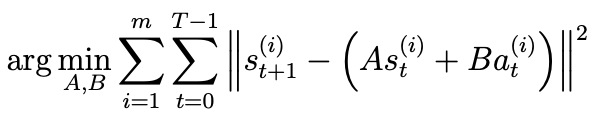
- A와 B를 학습한후, 다음 상태 s_t+1를 결정하는 방법에는 두 가지가 존재한다.
1) deterministic model
- 주어진 s_t와 a_t에 대해 정확히 하나의 s_t+1를 출력하다.
2) stochastic model
- 다음과 같이 nosie term epsilon_t를 추가하여 모델링한다.
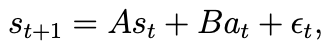
- 여기서 epsilon_t ㅌ N(o,COV)를 따른다.
- linear regression으로 학습할 수 있다면, non-linear regression도 가능하다.
- 예를 들어, s_t와 a_t에 대한 non-linear feature mapping을 적용할 수 있다.
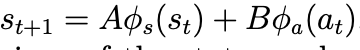
- 각각의 함수는 non-linear feature mapping을 하는 함수를 의미한다.
4.2. Fitted value iteration
- 이제 연속 MDP의 value function를 근사하는 방법에 대해서 알아보자.
- 이를, fitted value iteration이라고 한다.
- 우리는 이제 state space S가 연속적인 공간이며, activation space A는 작고 이산적이라고 가정하자
- value iteration은 다음과 같은 update를 수행한다고 하자.
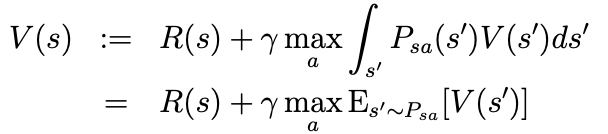
- 이를 다음과 같이 정의할 수 있다.
- fitted value iteration의 핵심 아이디어는 위의 update를 finite sample of states에서 근사적을 수행하는 것이다.
- supervised learning algorithm을 사용하여 value function을 state로 근사시킬것이다.
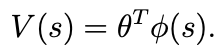
- 여기서 phi는 feature mapping을 의미한다.
- 각 state에서 fitted value iteration은 다음 값을 계산한다.
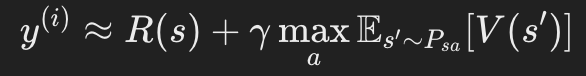
- 우리는 supervised learning algorithms을 적용하여 V(s)가 y에 가깝도록 학습시킨다.
- 알고리즘은 다음과 같다.

'DS Study > CS 229(Machine Learning)' 카테고리의 다른 글
| [CS229][17] Lecture 17 - MDPs & Value/Policy Iteration (1) | 2025.02.13 |
|---|---|
| [CS229] [16] Lecture 16 - Independent Component Analysis & RL (1) | 2025.02.09 |
| [CS 229] [15.5] Lecture 15.5 - PCA(principal Component Analysis) (0) | 2025.02.09 |
| [CS229] [15] Lecture 15 - EM Algorithm & Factor Analysis (0) | 2025.02.09 |
| [CS229] [14] Lecture 14 - Expectation-Maximization Algorithms (2) | 2025.02.08 |
