1. Introduction
1.1 sigma field
- 우선 sigma field에 대해서 미리 정의하고 가보자.(확률론의 베이스가 되니 알고가자.)

1.2. Definition [1] : Probability(확률)
- 확률은 다음과 같이 정의된다.
- C를 sample space라고 정의하고, B를 event들의 집합이라고 하자.
- 여기서 Probability Function P는 다음 조건을 만족해야 한다. (정의역이 B)
"""
i) Non-negativity
- P(A) >= 0, for all A ㅌ B
ii) Probability of sample space
- P(C) = 1
iii) Countable Additivity
- 합쳐지는 집합이 전부 disjoint할 때 다음을 만족해야 한다.

"""
- 이러한 Probability Function은 B 위에서의 확률이 어떻게 분포되어 있는지 나타낸다.
1.3. Theorem [1] : P(A) = 1 - P(A^c)
- 증명은 다음과 같이 할 수 있다.
proof)
- C = A U A^c and A n A^c =φ
- P(C) = P(A) + P(A^c) = 1
- 따라서, P(A) = 1 - P(A^c)
1.4. Theorem [2] : P(φ) = 0
- 증명은 위의 Theorem[1]에서 A = C라고 두면 자연스레 증명 가능하다.
1.5. Theorem [3] : A ㄷ B -> P(A) <= P(B)
- 증명은 다음과 같다.
proof)
- B를 다음과 같이 정리할 수 있다.

- 여기서 A, A^c n B는 disjoint하다.

- 그래서 P(B)를 합사건으로 전개 가능하다.

- 확률은 무조건 0이상이기 때문에 다음과 같은 조건을 만족한다.

1.6. Theorem [4] : 0 <= P(A) <= 1
1.7. Theorem [5] : P(A U B) = P(A) + P(B) - P(A n B)
proof)


- 여기서 P(A^c n B)에 대해 서로 같다라고 두면, 다음과 같이 식이 유도가 된다.

1.8. Definition [2] : Equilikely Case
- 모든 sample point가 같은 확률을 뛴다고 해보자.(C = {x_1,x_2,...,x_m}
- 이때, P(A)는 다음과 같이 정의된다.
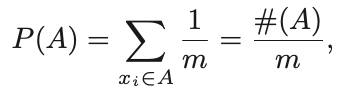
- 여기서 #(A)는 집합 A의 원소의 개수를 의미한다.
2. Counting Rules
- 간단하게 순열과 조합에 대해선 알고있다고 생각하고, 공식만 기술하고 넘어가보자.

- 여기서 조합은 다음과 같이 표현도 가능하다.
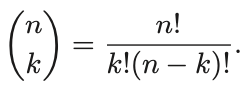
- 참고로, (a+b)^n의 각각의 계수도 combination으로 나타낼 수 있다.(이를 이항전개라고 한다.)

3. Inclusion Exclusion principle

- 이를 좀 더 일반화 하면 다음과 같다.
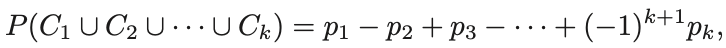
'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [6] Continuous Random Variables (0) | 2025.02.24 |
|---|---|
| [수리통계학] [5] Discrete Random Variables (1) | 2025.02.24 |
| [수리통계학] [4] Random Variables (0) | 2025.02.24 |
| [수리통계학] [3] Conditional Probability and Independence (0) | 2025.02.24 |
| [수리통계학] [1] Sets (0) | 2025.02.15 |
