1. Introduction
1.1. Definition [1] : Random Vector
- 예를 들어, 다음과 같은 vector가 있다고 생각해보자.
<영어성적,수학성적,학생 키>
- 각각의 parameter들은 전부 R.V.라고 말할 수 있는데,
- 이렇듯 n개의 R.V.를 vector로 표현한다면 이 vector를 random vector라고 부른다.
- Two R.V.의 cdf는 다음과 같이 나타내진다.

- 앞서서 우리는 R.V.를 알아보았을 때, pmf와 pdf을 정의했었는데,
- Random Vector에 대해서도 pmf와 pdf을 정의해보자.
- 이때 Random vector에 대해선 Joint pmf와 joint pdf로 joint가 그대로 이름에 붙게 된다.
- Joint pmf는 다음과 같다.

- 여기서 다음 두 조건을 만족해야한다.(기존의 pmf와 비슷)

- Joint pdf도 마찬가지로 Sumantion에서 Intergral로 바뀐 조건만 만족하면 된다.

- 여기서 joint cdf를 통해 joint pdf을 유도하려면 각 변수에 대해 편미분을 진행해주면 된다.

- 대략적인 joint pdf의 그래프는 다음과 같이 3차공간에 그려지게 된다.

2. Marginal Distribution
2.1. Difinition[1] : Marginal Distribution
- Random Vector (X,Y)가 있다고 해보자.
- 여기서 각각의 random variable에 대하여 probability을 정의할 수 있다.
- X와 Y중에 X에만 관심이 있고, Y에만 관심이 없다고 생각해보면,
- 다음과 같이 Probability을 구할 수 있다.
P(X = x)
= P(X = x , Y = y1 or X = x , Y = y2 or X = x, Y = y3,...)
= P(X = x, Y = y1) + P(X = x, Y = y2) + P(X = x, Y=y3) + ...
- random variable X에 대한 probability를 표현하고 있기에, X의 pmf라고 말 할 수 있다.
- 이렇듯, Random Vector에서 한개의 R.V. 에 대한 pmf를 Marginal pmf라고 불린다.
- cdf는 다음과 같이 나타낼 수 있다.

- 물론, Continuous R.V.에 대해선 다음과 같이 정의된다.

- Expectation은 다음과 같이 구할 수 있다.
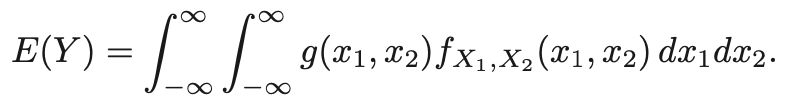

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [2.3] Conditional Distributions and Expectations (0) | 2025.02.28 |
|---|---|
| [수리통계학] [2.2] Transformations : Bivariate Random Variables (0) | 2025.02.28 |
| [수리통계학] [9] Important Inequalities (0) | 2025.02.27 |
| [수리통계학] [8] Some Special Expectations (0) | 2025.02.27 |
| [수리통계학] [7] Expectation of a Random Variable (0) | 2025.02.25 |
