1. Introduction
1.1. Difinition [1] : Covariance
- (X,Y)가 joint distribution을 가진다고 할때, 우리는 Covariance를 다음과 같이 정의할 수 있다.
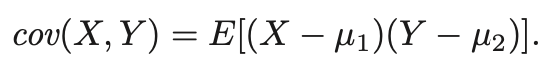
- 즉, 편차의 곱의 평균이라고 생각하면 되는데, 해당식을 풀면 다음과 같이 정리 가능하다.
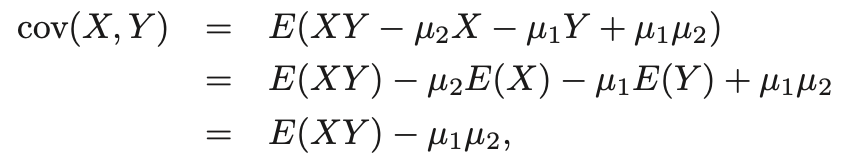
- 여기서, X,Y가 서로 independent하다면, E(XY) = E(X)E(Y)를 만족하게 되는데,
- 여기서 cov(X,Y) = E(X-mu1)E(Y-mu2)로 작성이되는데, 이는 각각 0 을 향하게 된다.
- 즉, cov(X,Y)가 0 이 된다.
- 다시 정리해서, X,Y가 서로 독립이면 Covariance는 0이다.
- 하지만, Covariance이 0이라고 해서 X,Y가 서로 독립이라곤 할 수 없다.
1.2. Difinition [2] : Correlation Coefficient
- 위에서 정의한 Covariance를 통해 Correlation Coefficient를 유도할 수 있다.
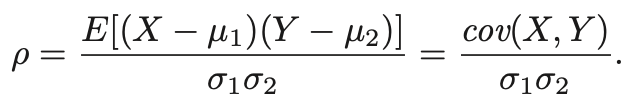
- Covariance는 R.V.에 따라서 나오는 값의 range가 달라지지만, Correlation Coefficient는 각각의 표준편차로 나눠주기 때문에,
- range가 [-1,1]로 Scaling된다.
- 여기서, Correlation Coefficient가 0보다 크면 양의 상관관계, 0보다 작으면 음의 상관관계를 가진다고 한다.
- [-1,1]로 Scaling되는 이유는 Cauchy-Schwarz Inequality를 이용하여 증명가능하다.
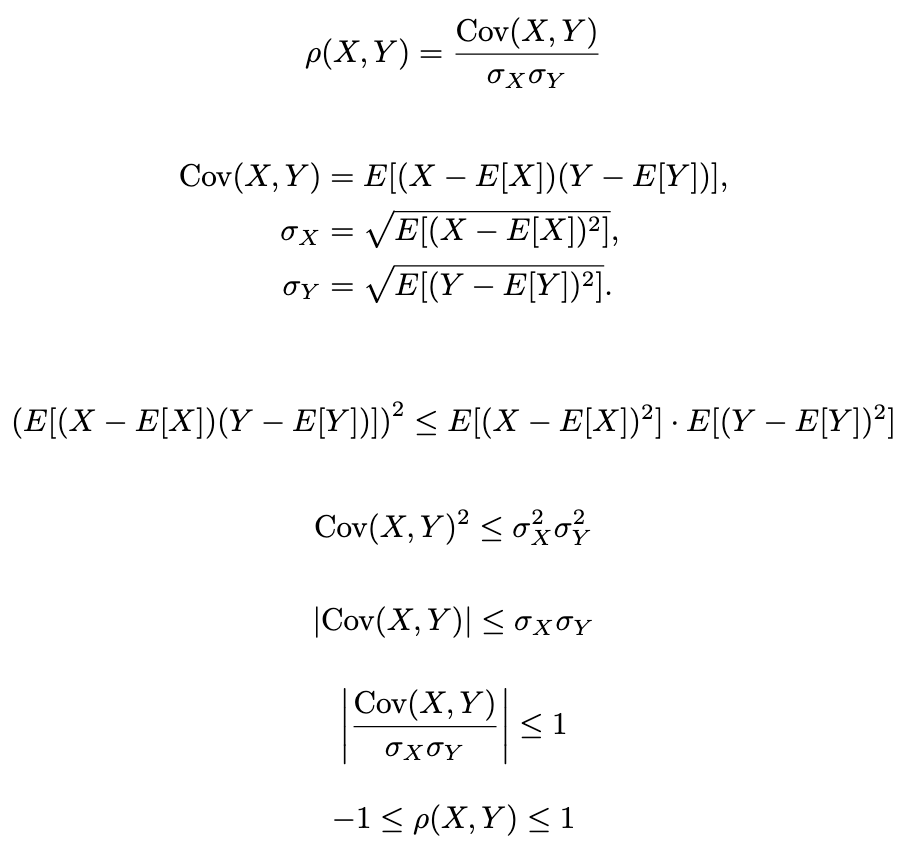
1.3. Theorem [1]
- E(Y | X)가 linear in X라고 가정해보자. (E(Y | X) = a + bX)꼴이 된다.
- 그러면 다음 식을 만족한다고 한다.
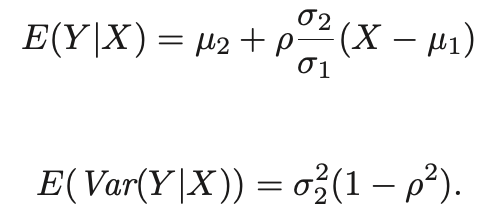
- 여기서 E(Y|X)를 통해서 a,b의 값을 얻어낼 수 있다.
- 우선 해당 식이 정말 만족하는지 증명을 통해서 알아보자.
- 우선 E(Y|X) 부터 증명해보자.

- 두 번째 식은 다음과 같이 증명 가능하다.
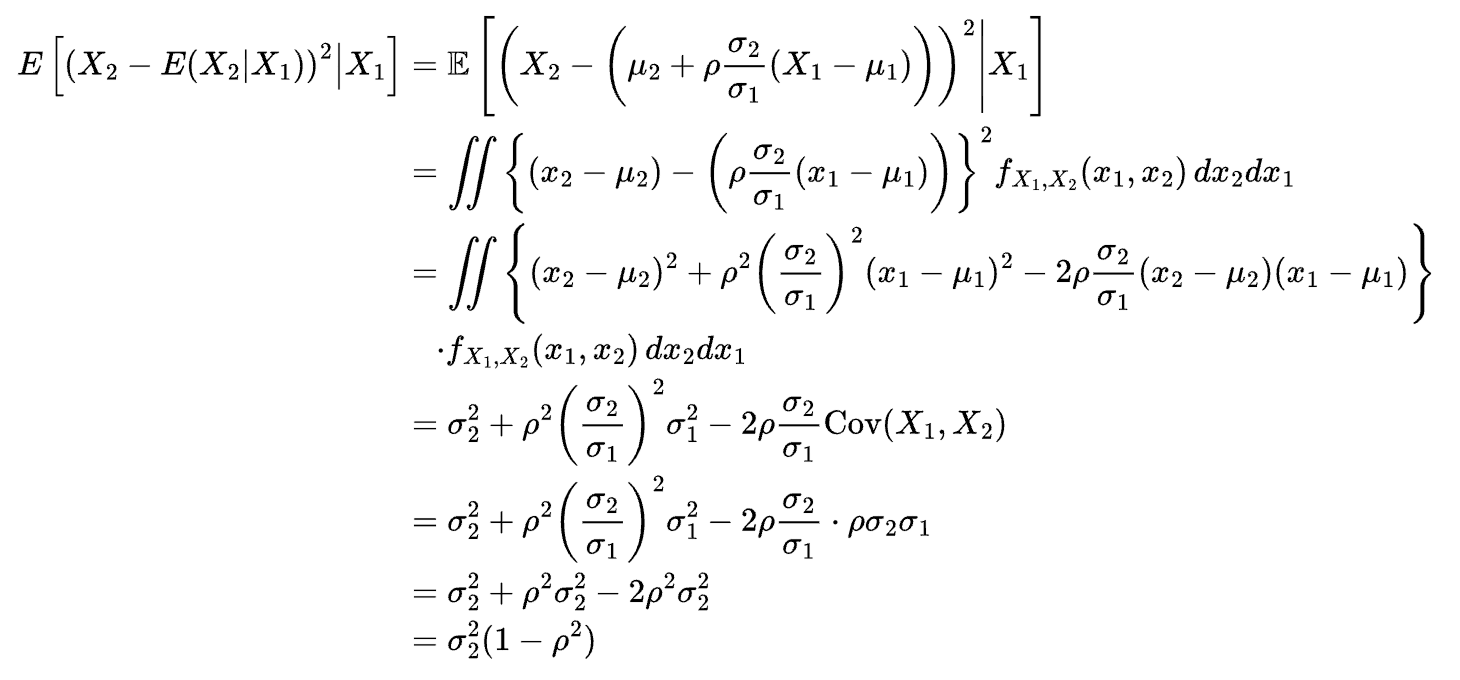
'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [2.7] Transformation for Several Random Variables (0) | 2025.03.02 |
|---|---|
| [수리통계학] [2.6] Extension to Several Random Variables (0) | 2025.03.01 |
| [수리통계학] [2.4] Independent Random Variables (0) | 2025.03.01 |
| [수리통계학] [2.3] Conditional Distributions and Expectations (0) | 2025.02.28 |
| [수리통계학] [2.2] Transformations : Bivariate Random Variables (0) | 2025.02.28 |
