1. Introduction
1.1. Definition [1] : Random Vector
- n개의 R.V.로 구성된 column vector를 다음과 같이 정의해보자.
X = (X1,...,Xn)^T : n-dim random vector라고 불림.
- 이걸 joint cdf로 나타내면 다음과 같이 표현 가능하다.
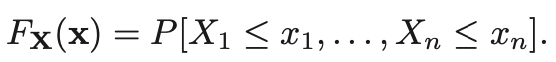

- 여기서 pdf를 구하고 싶으면 다음과 같이 편미분을 취해주면 된다.

- Y = u(x1,...,xn)라고 할때, E(Y)는 다음과 같다.

- marginal distribution도 다음과 같이 표현가능하다.

- conditional pdf는 다음과 같다.

1.2. Definition [2] : iid(independent identically distribution)
- 간단히, 각각의 R.V.가 independent하고, 전부 동일한 distribution에 속한다면,
- 이를 iid라고 불린다.
2. Multivariate Variance-Covariance Matrix
2.1. Definition [1] : Variance-Covariance Matrix
- 우리가 앞서서 Random Vector처럼 R.V.를 일차원으로 배열했었다면,
- 더 높은 차원으로 배열시키고자 나오게된 개념이다.
- 즉, R.V.를 Matrix로 배열하고자 하는 것이다.
- 이때 R.V. Matrix를 W라고 하자.
- 그러면 Expectation은 다음을 만족한다.

- Variance-Covariance Matrix는 다음과 같이 정의된다.

- 이름이 Variance-Covariance Matrix인 이유는
- 대각 원소가 Variance로 이루어져 있고, 나머지 원소들이 Covariance를 이루고 있기 때문에다

- 이를 바탕으로, 두 가지 정리가 나오게 된다.(증명은 생략하겠습니다. --> 간단하게 증명가능합니다.)

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [2.8] Linear Combinations of Random Variables (0) | 2025.03.02 |
|---|---|
| [수리통계학] [2.7] Transformation for Several Random Variables (0) | 2025.03.02 |
| [수리통계학] [2.5] The Correlation Coefficient (0) | 2025.03.01 |
| [수리통계학] [2.4] Independent Random Variables (0) | 2025.03.01 |
| [수리통계학] [2.3] Conditional Distributions and Expectations (0) | 2025.02.28 |
