1. Introduction
1.1. Difinition [1] : Bernoulli Distribution
- Bernoulli Experiment는 실험 결과가 두 가지 상호 배타적이고 포괄적인 방식으로 분류될 수 있는 확률 실험을 의미한다.
- 예를 들어, 성공 or 실패(생존 또는 사망, 불량 또는 정상)과 같은 경우가 있다.
- 베르누이 시행이 여러 번 독립적으로 수행되면서 성공할 확률 p가 일정하게 유지되는 경우, 이를 "Bernoulli Trials"라고 한다.
- 이러한 실험에서 각 시행의 성공 확률을 p라고 정의한다.
- R.V. X가 베르누이 시행과 연관되어 있을 때, X를 다음과 같이 정의한다.
- X(성공) = 1 , X(실패) = 0
- 즉, 성공과 실패라는 두 가지 결과를 각각 1과 0으로 나타낸다.
- pmf는 다음과 같이 표현되게 된다.

- 이때, X가 Bernoulli Distribution을 따른다고 한다.
- Bernoulli Distribution의 Expectation은 다음과 같다.

- 분산은 다음과 같다.

1.2. Binomial Distribution
- n개의 independent한 베르누이 시행이 수행될 때, 성공 횟수를 R.V X로 정의할 수 있다.
- 이 경우 X의 가능한 값은 0,1,2,3,...,n이 된다.
- n번의 시행에서 정확히 x번 성공할 확률을 계산하기 위해, x개의 성공을 선택하는 방법의 수를 고려해야 한다.
- 이는 Binomial coefficient로 표현되며 다음과 같다.

- 각 시행이 독립적이므로 성공과 실패의 확률이 각각 p와 1-p일 때, 특정 x번 성공할 확률은 다음과 같이 표현된다.

- 이때, X가 Binomial Distribution을 따른다고 한다.
- Binomial Distribution의 Expectation과 Variance는 다음과 같다.(구하는 과정 생략)
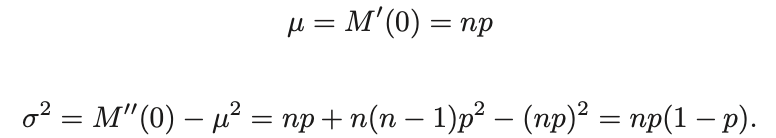
2. Negative Binomial and Geometric Distribution
- independent한 베리누이 시행이 연속적으로 수행되며 성공확률이 p로 일정하다고 가정하자.
- R.V Y를 r번 성공하기 전까지 발생한 실패 총 횟수라고 정의하자.
- 즉, Y + r이 전체 시행 횟수를 의미하게 된다.
- 이 때, R.V Y의 pmf는 다음과 같이 표현된다.

- 이때, y가 negative Binomial Distribution을 따른다고 볼 수 있다.
- 이 때, Expectation과 Variance는 다음과 같다.
- E(Y) = r/p
- V(Y) = r(1-p) /p^2
- negative Binomial Distribution에서 r = 1인 경우, Geometric Distribution이라고 정의한다.
3. Multinomial Distribution
- Multinomial Distribution은 Bernoulli Distribution과 Binomial Distribution의 확장판이라고 할 수 있다.
- 여러 개의 범주로 이루어진 확률 분포를 다룰 때 사용된다.
- 즉, 한번의 실험에서 결과가 여러 개의 범주 중 하나로 나뉘는 경우에 적용된다.
- Multinomial Distribution은 n번의 독립적인 시행에서 각 시행이 k개의 가능한 범주 중 하나로 분류될 확률을 모델링한다.
-- 각 범주에 대한 성공확률이 p1,p2,...,pk (총합이 1)
-- 총 n번의 시행 후 각 범주에서의 발생횟수를 X1,X2,...,Xk라고 할 때,
-- Random Vector(X1,X2,...,Xk)는 multinomial Distribution을 따르게 된다.
- 이 때, pmf는 다음과 같다.

- 이때, Expectation, Variance, Covariance는 다음과 같다.
- E[Xi] = np_i
- Var[Xi] = np_i(1-p_i)
- Cov(Xi,Xj) = -np_ip_j
4. Hypergeometric Distribution
- Hypergeometric Distribution은 비복원 추출(without replaement)방식에서
- 특정 조건을 만족하는 사건이 발생할 확률을 나타내는 이산 확률 분포이다.
- 예를 들면 다음과 같다.
- N명의 사람들이 있다고 가정하자. 이중 D명은 남자, N-D명은 여자라고 하자.
- 이때, n명의 사람을 골랐을 때, 남자가 몇 명인지 묻는 문제가 Hypergeometric Distribution를 따른다고 할 수 있다.
- N개에서 n개를 뽑는 경우의 수는 다음과 같다.

- 우리가 뽑은 크기 n인 표본 안에 우리가 원하는 원소 x개가 들어 있을 경우의 수를 구해보자.
- 모집단에 있는 D개 중에서 x개가 뽑혀야한다.
- 그리고, 나머지는 N-D개 중에서 n-x개가 뽑히면 된다.

- 이걸 종합하여 우리가 구하고자 하는 Hypergeometric Distribution의 pmf는 다음과 같다.

- Hypergeometric Distribution의 Expectation과 Variance는 다음과 같다.
E(X) = Dn/N

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [3.3] The Gamma,Chi-square, and Beta Distributions (0) | 2025.03.04 |
|---|---|
| [수리통계학] [3.2] The Poisson Distribution (0) | 2025.03.03 |
| [수리통계학] [2.X] 표본 분산에 n-1을 나눠주는 이유 (0) | 2025.03.02 |
| [수리통계학] [2.8] Linear Combinations of Random Variables (0) | 2025.03.02 |
| [수리통계학] [2.7] Transformation for Several Random Variables (0) | 2025.03.02 |
1. Introduction
1.1. Difinition [1] : Bernoulli Distribution
- Bernoulli Experiment는 실험 결과가 두 가지 상호 배타적이고 포괄적인 방식으로 분류될 수 있는 확률 실험을 의미한다.
- 예를 들어, 성공 or 실패(생존 또는 사망, 불량 또는 정상)과 같은 경우가 있다.
- 베르누이 시행이 여러 번 독립적으로 수행되면서 성공할 확률 p가 일정하게 유지되는 경우, 이를 "Bernoulli Trials"라고 한다.
- 이러한 실험에서 각 시행의 성공 확률을 p라고 정의한다.
- R.V. X가 베르누이 시행과 연관되어 있을 때, X를 다음과 같이 정의한다.
- X(성공) = 1 , X(실패) = 0
- 즉, 성공과 실패라는 두 가지 결과를 각각 1과 0으로 나타낸다.
- pmf는 다음과 같이 표현되게 된다.

- 이때, X가 Bernoulli Distribution을 따른다고 한다.
- Bernoulli Distribution의 Expectation은 다음과 같다.

- 분산은 다음과 같다.

1.2. Binomial Distribution
- n개의 independent한 베르누이 시행이 수행될 때, 성공 횟수를 R.V X로 정의할 수 있다.
- 이 경우 X의 가능한 값은 0,1,2,3,...,n이 된다.
- n번의 시행에서 정확히 x번 성공할 확률을 계산하기 위해, x개의 성공을 선택하는 방법의 수를 고려해야 한다.
- 이는 Binomial coefficient로 표현되며 다음과 같다.

- 각 시행이 독립적이므로 성공과 실패의 확률이 각각 p와 1-p일 때, 특정 x번 성공할 확률은 다음과 같이 표현된다.

- 이때, X가 Binomial Distribution을 따른다고 한다.
- Binomial Distribution의 Expectation과 Variance는 다음과 같다.(구하는 과정 생략)
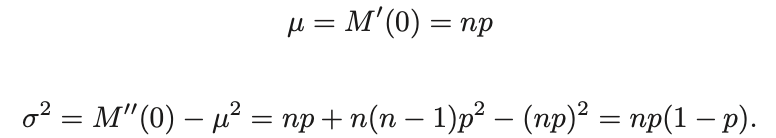
2. Negative Binomial and Geometric Distribution
- independent한 베리누이 시행이 연속적으로 수행되며 성공확률이 p로 일정하다고 가정하자.
- R.V Y를 r번 성공하기 전까지 발생한 실패 총 횟수라고 정의하자.
- 즉, Y + r이 전체 시행 횟수를 의미하게 된다.
- 이 때, R.V Y의 pmf는 다음과 같이 표현된다.

- 이때, y가 negative Binomial Distribution을 따른다고 볼 수 있다.
- 이 때, Expectation과 Variance는 다음과 같다.
- E(Y) = r/p
- V(Y) = r(1-p) /p^2
- negative Binomial Distribution에서 r = 1인 경우, Geometric Distribution이라고 정의한다.
3. Multinomial Distribution
- Multinomial Distribution은 Bernoulli Distribution과 Binomial Distribution의 확장판이라고 할 수 있다.
- 여러 개의 범주로 이루어진 확률 분포를 다룰 때 사용된다.
- 즉, 한번의 실험에서 결과가 여러 개의 범주 중 하나로 나뉘는 경우에 적용된다.
- Multinomial Distribution은 n번의 독립적인 시행에서 각 시행이 k개의 가능한 범주 중 하나로 분류될 확률을 모델링한다.
-- 각 범주에 대한 성공확률이 p1,p2,...,pk (총합이 1)
-- 총 n번의 시행 후 각 범주에서의 발생횟수를 X1,X2,...,Xk라고 할 때,
-- Random Vector(X1,X2,...,Xk)는 multinomial Distribution을 따르게 된다.
- 이 때, pmf는 다음과 같다.

- 이때, Expectation, Variance, Covariance는 다음과 같다.
- E[Xi] = np_i
- Var[Xi] = np_i(1-p_i)
- Cov(Xi,Xj) = -np_ip_j
4. Hypergeometric Distribution
- Hypergeometric Distribution은 비복원 추출(without replaement)방식에서
- 특정 조건을 만족하는 사건이 발생할 확률을 나타내는 이산 확률 분포이다.
- 예를 들면 다음과 같다.
- N명의 사람들이 있다고 가정하자. 이중 D명은 남자, N-D명은 여자라고 하자.
- 이때, n명의 사람을 골랐을 때, 남자가 몇 명인지 묻는 문제가 Hypergeometric Distribution를 따른다고 할 수 있다.
- N개에서 n개를 뽑는 경우의 수는 다음과 같다.

- 우리가 뽑은 크기 n인 표본 안에 우리가 원하는 원소 x개가 들어 있을 경우의 수를 구해보자.
- 모집단에 있는 D개 중에서 x개가 뽑혀야한다.
- 그리고, 나머지는 N-D개 중에서 n-x개가 뽑히면 된다.

- 이걸 종합하여 우리가 구하고자 하는 Hypergeometric Distribution의 pmf는 다음과 같다.

- Hypergeometric Distribution의 Expectation과 Variance는 다음과 같다.
E(X) = Dn/N

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [3.3] The Gamma,Chi-square, and Beta Distributions (0) | 2025.03.04 |
|---|---|
| [수리통계학] [3.2] The Poisson Distribution (0) | 2025.03.03 |
| [수리통계학] [2.X] 표본 분산에 n-1을 나눠주는 이유 (0) | 2025.03.02 |
| [수리통계학] [2.8] Linear Combinations of Random Variables (0) | 2025.03.02 |
| [수리통계학] [2.7] Transformation for Several Random Variables (0) | 2025.03.02 |
