1. Gamma Distributions
1.1. Gamma Function
- Gamma Distribution에 대해서 알아보기 전에, Gamma Function에 대해서 알고가보자.
- gamma function은 다음과 같다.(유도가 되는 함수가 아니라, 그냥 정의가 된 함수니 그러려니 하고 넘어가자)

- 이 gamma function의 성질은 다음과 같다.
i) alpha가 1보다 클 때, 다음을 만족한다.

- 해당 성질에 의해서 alpha가 자연수일 때 다음 성질을 가진다.

1.2. pdf of gamma
- R.V. X가 Gamma distribution에 속하는데, 모수가 alpha와 beta가 있다고 하자.
- X의 pdf는 다음과 같다.

- pdf의 motivation을 함께 알아보자.

- 양변을 gamma(alpha)로 나눠주면 다음과 같다.

- 적분 안에 있는 아이가 자연스레 gamma distribution의 pdf가 된다는 것을 알 수 있다.
1.3. mgf

- 이를 통해 평균과 분산을 구하면 다음과 같다.

1.4. Relationship with Poisson Distribution
- Gamma Distribution은 Poisson Distribution과 깊은 연관이 있다.
- 우선 R.V. W를 다음과 같이 정의하자.
W : time needed to obtain k changes(failures, deaths)
- G(w) = P(W <= w) = 1 - P(W > w) cdf of W
Note that
{ W > w } == less than k changes in (0,w)
Define
- R.V. X : # of changes in (0,w)
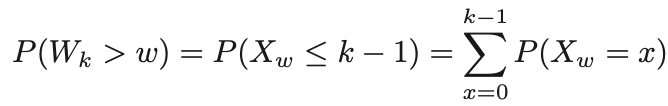
- 우리가 보이고 싶은건 다음과 같다.

- 이를 보이기 위해, 부분적분과 수학적 귀납법을 이용하여 증명한다.



2. Chi-square Distribution
2.1. Definition [1] : Chi-square Distribution
- Chi-square Distribution은 gamma distribution에서 alpha = r/2 , beta = 2일때를 따른다.

2.2. Definition [2] : Degree of Freedom(d.f.)
- X1,X2,X3가 있다고 생각해보자(각각 사람 키를 의미한다.)
- 이때, 아무 제약이없다면, X1,X2,X3는 모두 자유롭게 값을 가진다. (d.f. = 3)
- 하지만, 평균이 170이라고 제약이 주어진다면,
- X1,X2는 자유롭게 값을 가지지만, X3는 무조건 (510-X1-X2)의 값을 가진다.(강제)
--> d.f. = 3-1 = 2
- d.f = n - # of restrictions
2.3. mgf

- mu = d.f. (1번 미분)
- var = 2 * d.f. (2번 미분)
3.Beta Distribution
- Beta Distribution은 연속 확률 분포로, [0,1] 내에서 정의되는 R.V.의 Distribution을 나타낸다.
- 주로 Bayesian Statistics에서 Prior Distribution으로 자주 사용된다.
3.1. pdf
- beta distribution의 pdf는 다음과 같이 정의된다.

- 여기서 B(alpha,beta)는 다음과 같다.


'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [3.5] The Multivariate Normal distribution (0) | 2025.03.05 |
|---|---|
| [수리통계학] [3.4] The Normal Distribution (0) | 2025.03.04 |
| [수리통계학] [3.2] The Poisson Distribution (0) | 2025.03.03 |
| [수리통계학] [3.1] The Binomial and Related Distributions (0) | 2025.03.03 |
| [수리통계학] [2.X] 표본 분산에 n-1을 나눠주는 이유 (0) | 2025.03.02 |
