1. Introduction
1.1. Difinition [1] : Hypothesis
- Hypothesis는 크게 두가지로 나뉜다.
i) Mathematical Hypothesis : 참과 거짓이 명확한 가설
ii) Statistical hypothesis : 결과를 확실하게 낼 수 없는 가설
--> H0 : 귀무가설(negation) : Null hypothesis
--> H1 : 대립 가설 (assertion) : alternative hypothesis
----> 두가지를 이용하여 가설을 검정하게 된다.
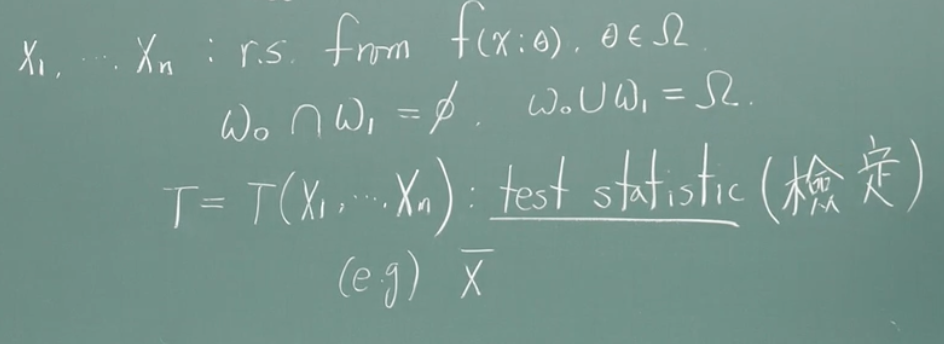
cf) test statistic : 검정통계량
- test statistic은 가설 검정을 위해 확률 분포를 결정하는 통계량이다.
1.2. Type I,II Error
- Type I Error : H0가 옳지만, 기각하는 오류
- Type II Errror : H0이 틀리지만, 채택하는 경우

- 이때 significance level과 Power of Test는 이를 수치화 하기 위해 사용되는데,
- definition은 다음과 같다.
"""
Significance level = P(rejectH0|H0) = P(Type I Error)
Power of Test = P(reject H0|H1) = 1 - P(Type II Error)
"""
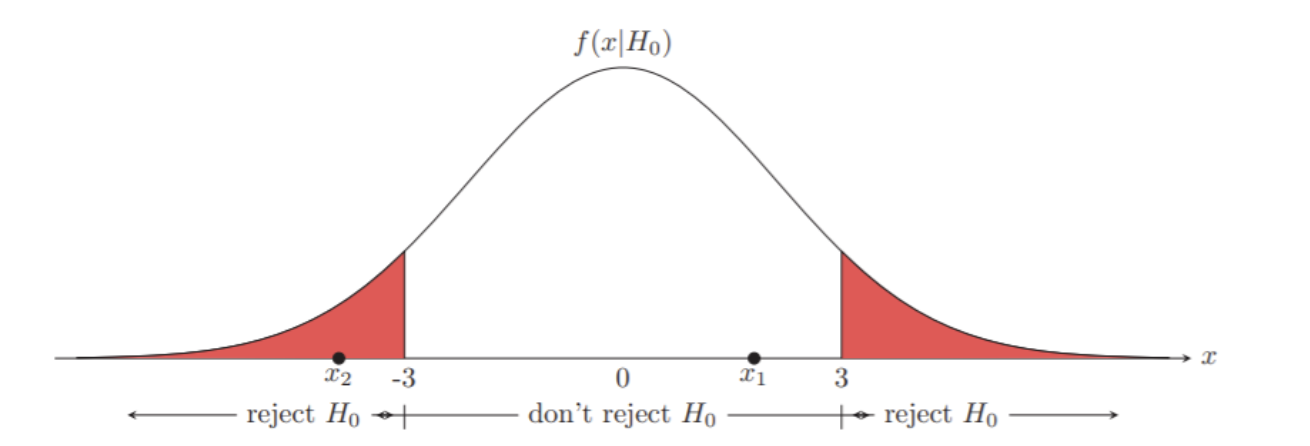
- 만일 Test statistic이 기각역에 속하면 H0을 기각하고,
- 아니라면, H0를 채택한다라는 판단이 가능하다.

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [4.7] Chi-square Tests (1) | 2025.03.06 |
|---|---|
| [수리통계학] [4.6] Additional Comments About Statistical Tests (0) | 2025.03.06 |
| [수리통계학] [4.4] Order Statistics (0) | 2025.03.06 |
| [수리통계학] [4.3] Confidence Intervals for Parameters of Discrete Distributions (0) | 2025.03.06 |
| [수리통계학] [4.2] Confidence Intervals (0) | 2025.03.06 |
