1. Introduction
1.1. Difinition [1] : Order Statistics
- Random sample X1,X2,...,Xn을 크기 순으로 다시 정리한
- random sample을 X1,X2,...,Xn의 ordered statistics이라고 부른다.
- 이를 작은 순서부터 Y1,Y2,...,Yn으로 표기해보자.
- 즉, Y1 은 Random sample중 가장 작은 값, Y2는 그다음으로 작은값,...Yn은 가장 큰값이 된다.
- 이러한 Order Statistics을 이용하여 다양한 statistics을 알아보자.
1.2. Difinition [2] : Sample Range

- Random sample의 정의역의 길이를 의미하며, 샘플들이 얼마나 분산되어 있는지 표현해주는 지표라고 생각하면 좋다.
1.3. Difinition [3] : Sample Median
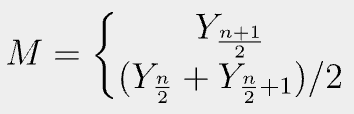
- 첫번째 식은 n이 홀수일때, 두번째식은 n이 짝수일때의 중앙값을 구하는 방법이다.
- 이상치가 많을경우 mean보다 median을 쓰는 경우가 더 적절할 때가 존재하다.
1.4. Difinition [4] : Sample Midrange
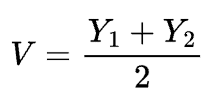
1.5. Difinition [5] : Sample Percentile
- 0 < p < 1 일 때, Probability Variable X의 p-분위수(Quantile of order p)는 값 ξ_p로 정의된다.
- 다음 조건을 만족한다.
- 이는 다른 말로 (100p)번째 백분위수(percentile)라고도 한다.
- 이를 통해 IQR이라는 되게 중요한 아이를 알게 되는데,
- Q1 : 25번째 백분위수
- Q2 : 50번째 백분위수 (중앙값과 동일
- Q3 : 75번째 백분위수 라고 정의하자.
- 그러면, IQR = Q3-Q1이라고 정의하자.
- 우리는 이 IQR을 이용하여 분포의 spread 또는 산포도를 나타내는 척도로 사용 가능하다.
1.6. pdf

1.7. Box plot
- Box plot
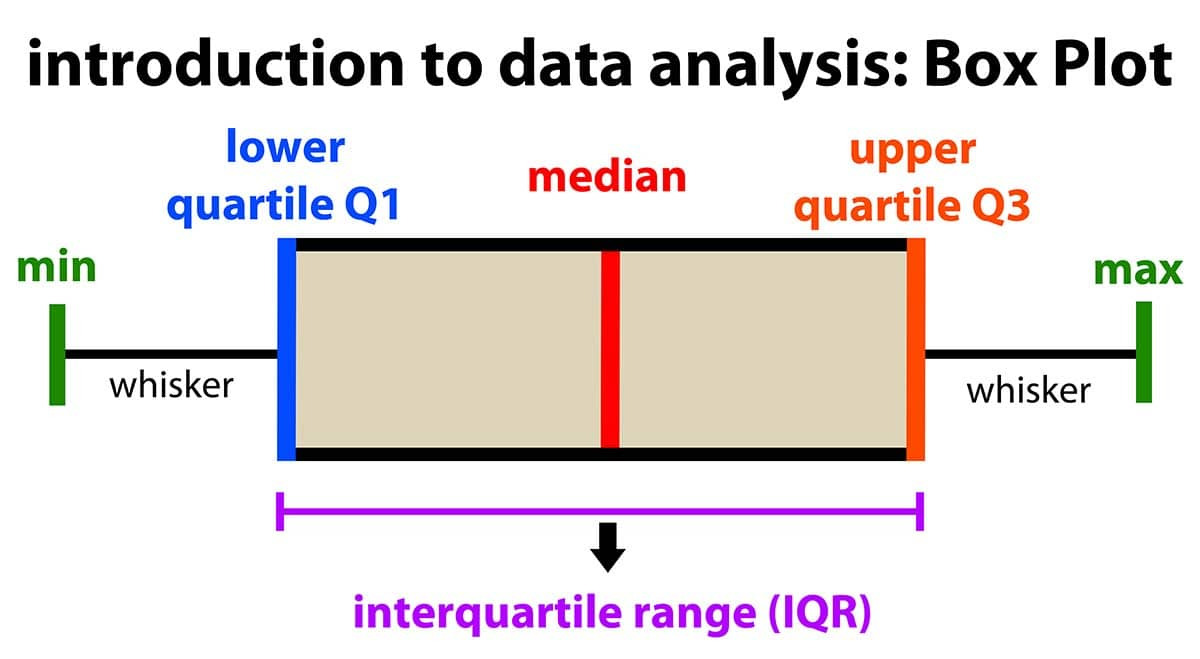
- Box-Whisker plot
--> LF,UF을 정한다.
- LF = Q1-h
- UF = Q3 +h
h = 1.5(Q3-Q1) = 1.5IQR
- LF, UF에 벗어나는 아이들을 이상치라고 볼 수 있다.

1.8. Q-Q plot(Quantile vs Quantile plot)
- 첫 번째 Q : 특정 분포의 분위수
- 두 번째 Q : 표본의 분위수
--> 만일 표본이 특정 분포를 정확히 따르면 y=x에 근사하게 된다.

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [4.6] Additional Comments About Statistical Tests (0) | 2025.03.06 |
|---|---|
| [수리통계학] [4.5] Introduction to Hypothesis Testing (0) | 2025.03.06 |
| [수리통계학] [4.3] Confidence Intervals for Parameters of Discrete Distributions (0) | 2025.03.06 |
| [수리통계학] [4.2] Confidence Intervals (0) | 2025.03.06 |
| [수리통계학] [4.1] Sampling and Statistics (0) | 2025.03.05 |

