1. Introduction
- 만일 R.V가 continuos R.V라고 한다면, P(X = 0) = 0 이 될 것이다. 즉, 어느 특정 점의 확률은 0일 수 밖에 없다.
- 따라서, 우리가 필요한 것은 추정치의 오차를 측정하는 방법이다.
- 즉, 추정치가 실측값을 얼마나 벗어났는지 평가할 수 있어야 한다.
- 해당 섹션에서는 오차의 추정치를 confidence interval의 개념을 이용해 표현할 것이다.
1.1. Definition [1] : Confidence Interval
- 표본 X1,X2,...,Xn이 R.V X에서 추출된다고 해보자.
- 여기서 X는 pdf f(x;theta)를 가지며, theta는 모르는 값이라고 하자.
- 0 < alpha < 1이라고 해보자.
- 두 통계량 L = L(X1,...Xn) , U = U(X1,...,Xn)이 주어졌을 때,
- 만약 다음 조건을 만족한다면 구간 (L,U)를 (1-alpha)100% confidence interval이라고 한다.

1.2. Difinition [2] : t-interval, standard error
- X1,...,Xn이 N(mu,sigma^2) distribution을 따르는 R.V라고 하자, sample mean과 sample variance를 각각 구하게 되면,

- R.V T는 degree of freedom이 n-1인 t-distribution를 따르게 된다.
- 이를 이용하여 다음과 같이 신뢰구간을 구할 수 있다.
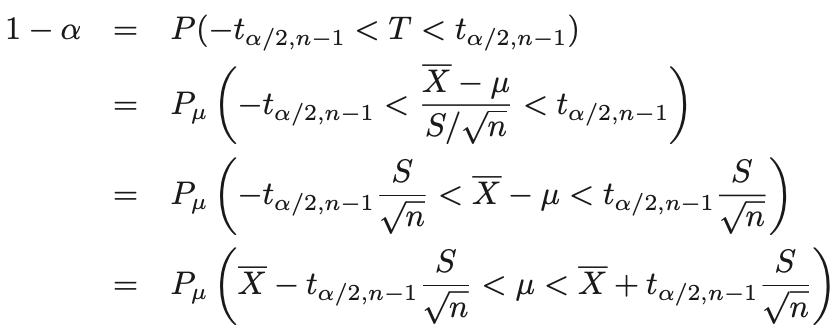
- confidence interval를 구하면 다음과 같다.
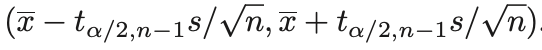
- 이를 t-interval이라고 하며, S/sqrt(n)을 standard error(표준오차)라고 한다.
1.3. Difinition [3] : Central Limit Theorem(CLT)
- 증명은 Chapter 5에서 하게 된다.
- 하지만,개념만 설명하자면 다음과 같다.
- 표본 평균의 분포가 모집단이 어떤 분포를 보이든 간, 무조건 Normal Distribution에 가까워 진다는 것을 의미한다.
- 표본의 크기가 충분히 크다면(30이상), CLT에 의해 표본평균의 분포가 Normal Distribution에 가까워진다.
- 따라서 다음과 같이 Confidence Interval를 구할 수 있다.


2. Confidence Intervals for Difference in Means
- 해당 파트에선, 두 분포를 비교하게 될건데, 두 개의 R.V X와 Y의 분포를 비교하게 될 것이다.
- X와 Y의 평균을 비교하는 방식에 대해서 알아갈 것이다.
- X와 Y의 평균을 각각 mu_1, mu_2라고 할 때, 다음에 대한 confidence interval를 구하게 될 것이다.
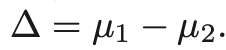
- X와 Y의 sample mean을 다음과 같이 정의하자.
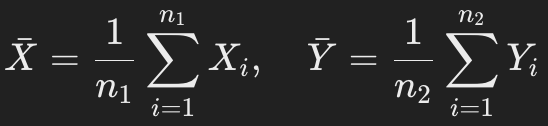
- 그리고 차이를 다음과 같이 정의하자.
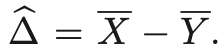
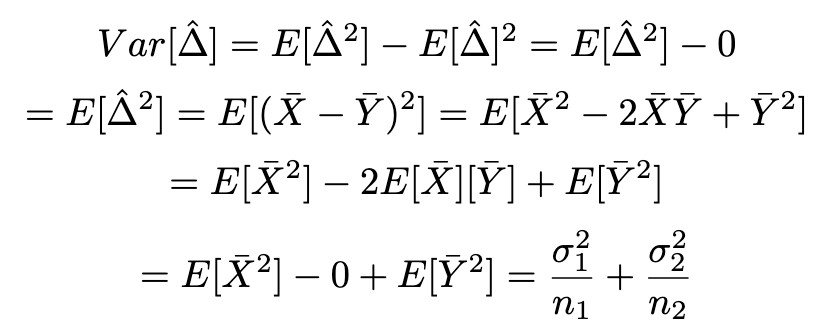
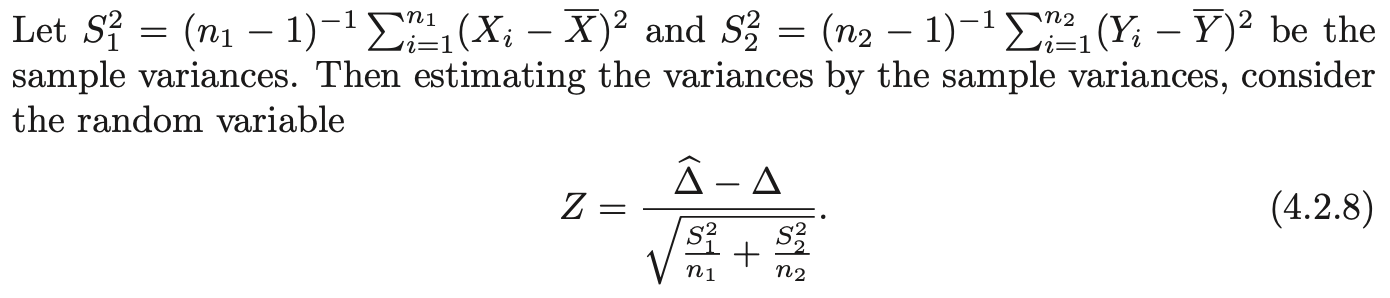
- Confidence Interval은 다음과 같다.

- 이번엔 X,Y가 동일한 분산을 가진다고 가정하자, 즉, sigma1^2 = sigma2^2인 경우를 의미한다.
- 여기서 T 통계량은 다음과 같다.
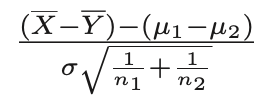
- 분산에 대한 estimator를 정의해야하는데, 여기선 가중평균을 사용하여 pooled estimator를 다음과 같이 정의한다.
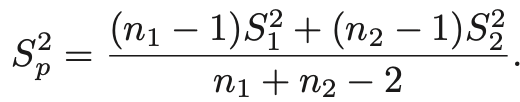

- confidence interval은 다음과 같아진다.
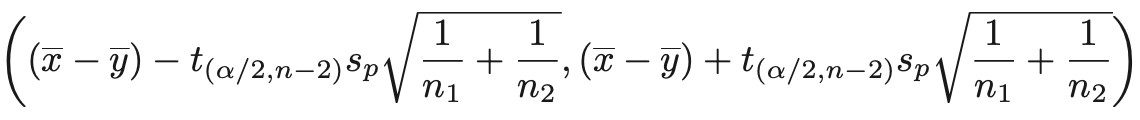
'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [4.4] Order Statistics (0) | 2025.03.06 |
|---|---|
| [수리통계학] [4.3] Confidence Intervals for Parameters of Discrete Distributions (0) | 2025.03.06 |
| [수리통계학] [4.1] Sampling and Statistics (0) | 2025.03.05 |
| [수리통계학] [3.6] The t and F distribution (0) | 2025.03.05 |
| [수리통계학] [3.5] The Multivariate Normal distribution (0) | 2025.03.05 |
