1. Introduction
1.1. Random number generation
- 밑의 정리는 Monte Carlo에서 가장 중요한 정리중 하나이다.
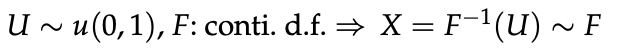
- 증명은 다음과 같이 할 수 있다.
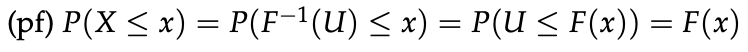
- 해당 정리를 이용하여, ㅠ를 추정할 수 있다.
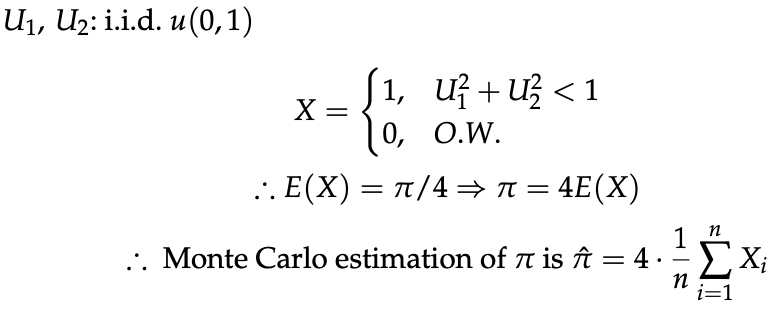
1.2. Monte Carlo intergration

- 직접 적분을 하지 않더라도, E(g(x))만 구할 수 있다면 정적분을 계산 할 수 있다.
- 저렇게 Expectation으로 바뀌는 이유는 1/(b-a)가 uniform distribution의 pdf이기 때문이다.
1.3. Box-Muller Transformations
- Uniform distribution을 Normal distribution으로 mapping시키는 기법이다.
- 우선 다음과 같이 R.V U1,U2가 Uniform distribution을 따른다고 가정하자.
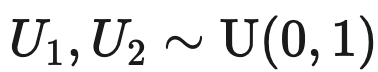
- 그후 우리가 유도하고자 하는 R.V X1,X2를 Normal distribution을 따른다고 가정해보자.

- X1,X2를 좌표에 놓고 극좌표를 구하게 되면 (R,theta)가 되는데, 다음과 같이 표현 가능하다.
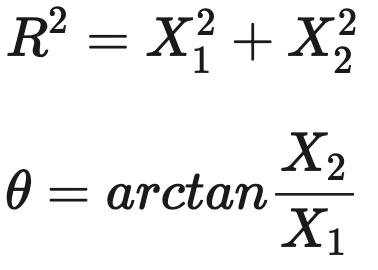

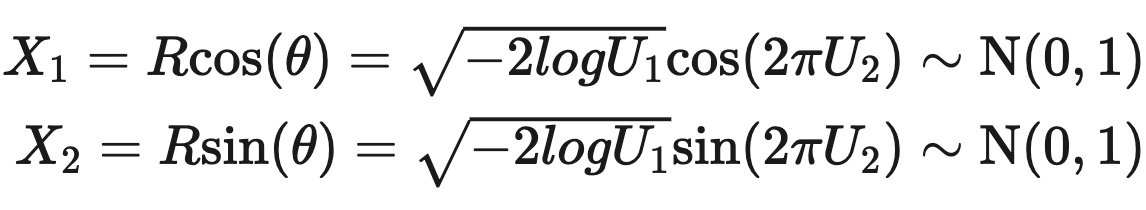
1.4. Accept-reject Method
- Accept-reject method는 간단하게 설명하자면,
- 간단하게 샘플링할 수 있는 분포를 이용하여 샘플링하기 어려운 분포를 생성하는 것을 의미한다.
- https://angeloyeo.github.io/2020/09/16/rejection_sampling.html
Rejection Sampling - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
- 해당 포스팅을 참고하면, 아주 잘 설명이 되어있다
. 나는 증명 위주로 포스팅하겠다.


'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [5.1] Convergence in Probability (0) | 2025.03.09 |
|---|---|
| [수리통계학] [4.9] Bootstrap Procedures (0) | 2025.03.09 |
| [수리통계학] [4.7] Chi-square Tests (1) | 2025.03.06 |
| [수리통계학] [4.6] Additional Comments About Statistical Tests (0) | 2025.03.06 |
| [수리통계학] [4.5] Introduction to Hypothesis Testing (0) | 2025.03.06 |
