1. Fisher information
1.1. additional regularity condition
- 기존에 MLE을 정의하기 위한 regularity condition에서 추가적으로 두가지 제약이 더 생긴다.
i) R0 : The cdfs are distinct. (밑의 수식을 의미한다.)
ii) R1 : The pdfs have common support for all theta.
iii) R2 : The point theta_0 is an interior point in OMEGA
iv) R3 : f(x : theta) is twice differentiable w.r.t. theta
v) R4

1.2. Bartlett identity
- 우선 pdf을 적분하면 1이 나온다는 것을 이용하여 양변을 미분해준다.

- 그 후 한번더 양변을 미분해보자.

- 마지막 I(theta) = Var(~~) = E(~~^2) - E(~~)^2 = E(~~^2) - 0 으로 유도 가능하다.
- I(theta) : Fisher information이라고 정의한다.
1.3. information for a location family

- theta는 단순히 distribution의 location을 이동시키는 역할을 한다.
- 즉, distribution의 형태는 동일하지만, 위치만 theta만큼 이동하게 된다.
- Location family는 분포의 형태는 유지되면서 위치만 이동하는 분포군을 의미한다.
1.4. Information fo random sample
- Fisher information도 joint 한 Random Sample에 대하여 다음과 같이 계산 가능하다.

- 즉, random sample의 개수만큼 정보가 더해지게 된다.
1.5. Rao-Cramer Lower Bound(RCLB)
- Random Sample X1,...,Xn이 있다고 가정하자.(앞에서 언급한 regularity condition 5개를 전부 만족)
- 다음과 같은 정리를 RCLB라고 정의한다.

- 즉, 최소한의 한계가 존재한다라는 것을 의미한다.
- 증명은 다음과 같다.


- 요기서 k'(theta) = E(Yz)와 같은데, 여기서 다음공식을 사용해준다.(Cov(Yz) = E(Yz)-E(Y)E(z))
- k'(theta) = E(Yz) = Cov(Yz) + E(Y)E(z) = Cov(Yz) + 0 = Var(Yz)
- Var(Yz)는 Correlation coefficient를 통해 유도해보면 다음과 같다.


- 만일 Y가 Unbiased Estimation일 경우, k(theta) = theta가 되기 때문에, k'(theta) = 1이 된다.
- 즉, 다음과 같다.

1.6. Efficiency
- 분산이 얼마나 작은가에 대한 효율성이라고 생각하면 편하다.
- definition은 다음과 같다.
- 만약 VAR(Y) = (n*I(theta))^-1과 같다면,
- An unbiased estimation Y를 Efficent Estimation이라고 부른다.
- 여기서, The efficiency of an unbiased estimation Y는 다음과 같다.

1.7. Asymptotic Normality of MLE
- 추가적으로 한가지 더 Regularity Condition이 추가된다.
- pdf가 theta에 대해 세번 미분가능하고, 모든 theta ㅌ Omega에 대해 상수 c와 함수 M(x)가 존재하여 다음을 성립한다.


- 한가지 정리가 나오게 되는데, 그 정리는 다음과 같다.
- X1,...,Xn이 pdf f(x ; theta_0)를 가지는 iid이고, theta_0 ㅌ Omega이며, R0~R5까지 만족한다고 하자.
- 추가로 Fisher Information I(theta_0)가 0 < I(theta_0) < Inf를 만족한다고 가정하자.
- 그러면, MLE의 일관된 solutions의 sequence가 다음을 만족하게 된다.
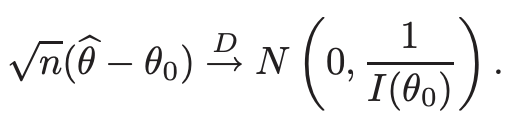
- 증명은 다음과 같이 할 수 있다.
"""proof
l'(theta)를 theta_0을 중심으로 2차 테일러 급수로 전개하여, theta^에 대해 다음과 같아진다.

- 여기서 theta*를 theta_0와 theta^의 사이의 값이라고 정의해보자.
- l'(theta^) = 0이므로 (MLE에서 최댓값이 되는 지점이기에, 무조건 0) 다음과 같이 정리할 수 있다.

- CLT에 의해서 다음과 같다.




"""
1.8. asymptotic efficiency
(i) definition

1.9. Asymptotic confidence interval


1.10. Newton-Raphson method
- gradient descent에 비해서 Newton's method은 훨씬 적은 반복으로 좋은 근사값을 얻을 수 있다.
- Newton's method은 특이한게, f(theta)=0을 만족하는 theta을 찾는다. 즉, 해를 찾는다는 것을 의미한다.
- 이걸 활용하면 f'(theta) = 0을 만족하는 즉, lost function을 minimize하는 점을 찾는 알고리즘으로도 사용가능할수도 있다.
- 단, Newton's method는 중근이나 사중근처럼 관통하지 않는 해를 구하는건 불가능하고, 무조건 관통하는 해여야한다.
- 다음과 같이 접선의 방정식을 구해서 그 방정식의 x 절편을 구하고
- 다시 그 x절편을 기준으로 접선의 방정식을 구해서 이와같은 방식을 반복하는 것이다.
- 이를 식으로 나타내면 다음과 같다.
- 여기서 Newton's method는 "Quadratic convergence"의 특징을 가지고 있다.
- 이는, 오차가 0.01, 0.0001, 0.00000001... 제곱의 단위로 줄어든다는 것을 의미한다.
'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [6.4~6.5] Multiparameter Case : Estimation,Test (0) | 2025.03.13 |
|---|---|
| [수리통계학] [6.3] Maximum Likelihood Test (0) | 2025.03.13 |
| [수리통계학] [6.1] Maximum Likelihood Estimation (0) | 2025.03.09 |
| [수리통계학] [5.3] Central Limit Theorem(CLT) (0) | 2025.03.09 |
| [수리통계학] [5.2] Convergence in Distribution (0) | 2025.03.09 |




