1. Likelihood Ratio Test(LRT)
1.1 definition

- 위와 같이 random sample이 주어져 있다고 가정하자.
- 우리가 검정할 것은 다음과 같다.
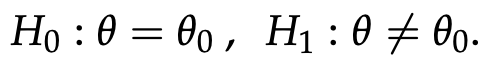
- 그리고, MLE에 해당하는 theta값을 다음과 같이 정의하자.
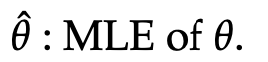
- 그리고 Likelihood ratio를 다음과 같이 정의해보자.(LRT에서의 test statistics가 된다.)

- 만약 귀무가설이 참이라면 Likelihood ratio는 1에 가까워 질것이고,
- 만약 대립가설이 참이라면 Likelihood ratio는 0에 가까워 질것이다.
- 이러한 motivation을 토대로, c를 기준으로 값이 작다면 귀무가설을 기각시키는 판단이 가능하다.

2. Wilks' Theorem
- Regularity condition R0~R5까지 만족한다고 가정하자.
- 여기서 wilks'Theorem은 다음과 같다.
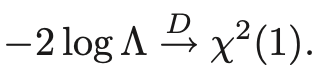
- 이를 한번 증명해보자.
- 우선, MLE of theta를 다음과 같이 정의하자.
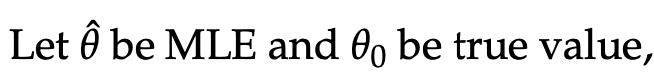
- 그리고 다음 식을 테일러전개로 식전개를 해보자.

- 여기서 다음을 만족하게 된다.


-위의 식을 만족하기 때문에, 다음과 같이 증명이 가능하다.

3. Wald and Score test

'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [7.1] Measures of Quality of Estimators (0) | 2025.03.14 |
|---|---|
| [수리통계학] [6.4~6.5] Multiparameter Case : Estimation,Test (0) | 2025.03.13 |
| [수리통계학] [6.2] Rao–Cramer Lower Bound and Efficiency (0) | 2025.03.11 |
| [수리통계학] [6.1] Maximum Likelihood Estimation (0) | 2025.03.09 |
| [수리통계학] [5.3] Central Limit Theorem(CLT) (0) | 2025.03.09 |
