1. Introduction
1.1. Likelihood Function

- likelihood는 간단하게, 추정하고자하는 모수가 모집단의 분포에 대해 가능한지에 대한 여부를 체크해주는 아이라고 생각하면 된다.
1.2. Regularity Conditions
- MLE를 정의하기 전에 제약조건 3가지가 필요하다.
i) R0 : The cdfs are distinct. (밑의 수식을 의미한다.)

ii) R1 : The pdfs have common support for all theta.
iii) R2 : The point theta_0 is an interior point in OMEGA
1.3. Theorem [1]
- R0,R1에 의해서 나오게 되는 중요한 정리는 다음과 같다.(theta0 == True parameter)
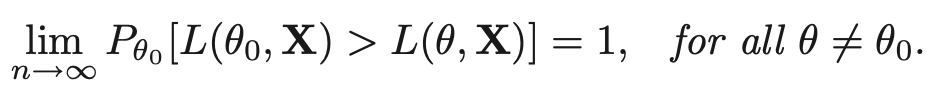
- 증명은 다음과 같다.

1.4. Theorem [2] : Maximum Likelihood Estimation
- MLE은 다음과 같다.

- Likelihood가 최대가 되는 지점은 간단히, 미분을 통해서 구해주면 된다.(고등학교 때 최대값 찾는 것처럼)
'Statistic Study > Mathematical Statistics(수리통계학)' 카테고리의 다른 글
| [수리통계학] [6.3] Maximum Likelihood Test (0) | 2025.03.13 |
|---|---|
| [수리통계학] [6.2] Rao–Cramer Lower Bound and Efficiency (0) | 2025.03.11 |
| [수리통계학] [5.3] Central Limit Theorem(CLT) (0) | 2025.03.09 |
| [수리통계학] [5.2] Convergence in Distribution (0) | 2025.03.09 |
| [수리통계학] [5.1] Convergence in Probability (0) | 2025.03.09 |
