0. Intro
- 선형 대수학에서 해집합(Solution Set)은 되게 중요하다.
- 이러한 해집합(Solution Set)을 벡터(Vector)표기법을 이용하여
- 기하적으로 해석하는 시간을 이번 챕터에서 다뤄볼까 한다.
1. Homogeneous Linear Systems
- 선형 연립방정식(Linear System)에서 특별한 형태를 한번 살펴보자.
- 어떠한 행렬 방정식(Matrix Equation)이 영벡터(zero vector) 일때
- 우리는 해당 방정식을 homogeneous equation 이라고한다.
- 여기서 해집합(Solution Set) 이 영벡터(zero vector) 뿐이라면 tirivial solution 이라고 하고
- 이외의 해집합을 갖는다면 이를 nontirivial solution 이라고한다.
- 이때 nontrivial solution을 갖는다는 것은 해당 해집합(Solution set)이 적어도 하나의 free variable을 갖게 된다.

- 반대로 행렬 방정식(Matrix Equation)이 영벡터(zero vector)가 아니라면
- 이를 nonhomogeneous equation 이라고 한다.

- 몇가지 문제를 같이 살펴보자.
Q1)
- 다음 homogeneous system이 nontrivial solution을 가지는지 판단하시오.
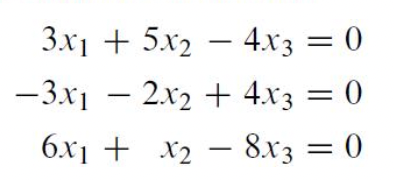
A1)
- 해당 문제를 풀기 위해 해당 선형연립방정식(Linear System)을 강화행렬(Augemented Matrix)로 나타내어
- row operation을 통해 RREF 을 구하여 해집합(Solution set)을 구하기 쉽게 변형 해보자.

-나오게된 RREF를 통해서 다음과 같은 식을 도출할 수 있다.

- x3 는 free variable 이라는 것을 알 수 있기에 이를 해집합(Solution set)으로 나타내면 다음과 같다.

- 이를 v에 대한 선형결합(linear combination) 과 같기 때문에 Span{v} 와 같다고 생각해도 무관하다.
Q2) 주어진 선형방정식의 해 집합을 구하시오

- 해당 식에서 x2, x3를 free variable로 잡을 수 있다.
- 그러면 해집합은 다음과 같아 질것이다.

- 해당 해집합을 자세히 살펴보면 벡터 u,v의 선형결합(linear combination)으로 나타나낼수 있음을 알수 있다.
- 즉 Span{u,v} 라는 것이다.
- 이를 기하적으로 표시하면 다음과 같다.

2. Parametric Vector Form
- 앞서 풀었던 Q2의 해집합을 나타냈던 표현에 대해 다시 살펴보자.

- 다음과 같이 벡터들끼리의 선형결합(linear combination)으로 나타낸 해집합(Solution set)을
- Parametric Vector Form 이라고 한다.
2.1. Nonhomogeneous Equation 에 대한 내용
- Nonhomogeneous Equation의 해집합과 homogeneous Equation의 해집합은 서로 평행관계이다.

'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-8] Introduction to Linear Transformations (2) | 2024.06.03 |
|---|---|
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-3] Vector Equations (0) | 2024.05.31 |
| [Linear Algebra] [1-2] Row reduction & Echelon Forms (0) | 2024.05.31 |

