0. Review
- 1-2 에서 우리는 어떤 행렬(Matrix)을 Row operation을 이용해
- RREF를 만들어 해 집합(Solution Set)을 도출해내는 방법에 대해 알았다.
- 이번 1-3에서는 선형 연립방정식(Linear System)을 벡터(Vector)로 나타내는 방법에 대해서 알아보자.
1. 벡터(Vectors)
- 해당 챕터에 본격적으로 들어가기 전에 벡터(Vector)에 대해서 알아보자.
- vector 는 당분간 "수의 순서쌍" 이라고 정의하자.
- 행렬에서 하나의 열(column)을 우리는 열 벡터(column vector)라고 지칭하고,
- 이를 단순하게 우리는 벡터(vector)라고 부를것이다.
ex)

1.1. 벡터 연산 (Vectors Operation )
- 벡터들끼리 연산이 가능한데 크게 두가지로 나뉜다. (내적, 외적 등등은 다음에 다룰것이다.)
i) 벡터 합 (Vector Sum)
ex)

ii) 스칼라 곱(Scalarmultiple)
ex)

Q)

A)

2. 기하적 의미(Geometric Descriptions of R^n)
- 좌표평면 위에 어느 한 점(a,b)가 있다고 생각해보자.
- 이 (a,b)를 가르키는 화살표, 즉 방향이 벡터를 의미한다.
ex)

- 여기서 벡터에 속하는 원소들의 개수가 차원의 개수를 의미하게 된다.
- 만약 a = <1,2,3> 이라면 a는 R^3 안에 속한다.
ex)

2.1. 벡터 합의 평행사변형 법칙(Parallelogram Rule for Addition)
- 벡터의 합을 기하적으로 한번 분석해보자.

- 다음과 같이 벡터 2개가 주어져있다고 생각해보자. 이 두개의 벡터를 더한건 다음 그림과 같다.

- 즉, 두개의 벡터의 합은 두벡터로 이루어진 평행사변형의 대각선과 같다는 것을 확인할 수 있다.
- 이를 벡터 합의 평행사변형 법칙(Parallelogram rule for addition)이라고 한다.
3. 대수적 성질(Algebraic Properties of R^n)
- n차원에서의 대수적 성질(Algebraic Properties)는 다음과 같다. (증명은 생략)

4. 선형 결합(Linear Combination)
- 지금까지 벡터 합(Vector sum) , 스칼라 곱(Scalar mulitple)에 대해 잡고 갔는데,
- 두 개념에 의하여 선형 결합(Linear Combination)이라는 중요한 개념이 나오게 된다.
- 이에 대해 알아가 보자.
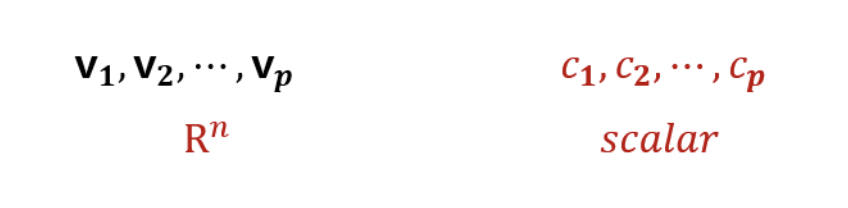
- 다음과 같이 벡터(Vector)와 스칼라(Scalar)가 주어져 있을 때
- 이를 이용해 벡터 합(Vector Sum), 스칼라 곱(Scalar multiple)을 이용하여 어떠한 다른 벡터(Vector)를 만들어 갈때
- 이 과정을 선형 결합(Linear combination)이라고 한다.
ex)

- 선형 결합(Linear combination)에 관련된 문제(Question)을 한번 풀어보자.
Q)

다음과 같이 벡터 3개가 주어져 있을 때, a1,a2벡터들을 선형 결합(Linear combination) 했을 때
b벡터를 만들수 있는지 없는지 판단하시오.
A)
- 우선 a1,a2 벡터들의 선형결합이 b벡터와 같다는 식을 세워보자.


- 결국 우리는 다음과 같은 연립방정식의 해를 구하는 것과 같을 것이다.

- 이를 증강행렬(Augmented Matrix)로 나타내고 row operation을 통해 RREF을 구하여 해집합(Solution Set)을 구해보자.

- 즉, (x1,x2) = (3,2) 가 된다.
4.1. 벡터방정식(Vector Equation)
- 우리는 해당 문제의 풀이 중에서 해당 식에 집중해보자

- 이렇게 벡터들의 선형결합(LInear combination)을
- 이용하여 방정식으로 나타낸 것을 벡터방정식(Vector Equation) 이라고 한다.
- 이를 증강행렬(Augmented Matrix)로 나타내면 다음과 같다.

5. Span
- 선형결합(Linear Combination)을 나타낸 식을 다시한번 살펴보자.

- 여기서 v1,..vp를 선형결합(linear Combination)을 했을 때 나올수 있는 모든 y벡터들의 집합을
- Span{v1,v2,...vp} 라고한다.
5.1. Span의 기하적 의미

- 해당 그림만 보더라도 Span의 의미에 대해 알수 있을거라 생각하고
- 이해가 되지 않더라도 앞으로의 챕터에서 자세히 서술할 예정이다
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
|---|---|
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (0) | 2024.06.01 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-2] Row reduction & Echelon Forms (0) | 2024.05.31 |
| [Linear Algebra] [1-1] Systems of Linear equations (0) | 2024.05.30 |

