0. Review
- 1-5 챕터에서 우리는 homogeneous equation 에 대해서 알아 봤고,
- 그 해집합(Solution set)이 오직 영벡터(Zero Vector)만 가질때 trivial solution을 가진다고 한다.
- 반대로 다른 해도 가진다면 그땐 nontirivial solution이라고 하였다.
- 이번 챕터에서는 trivial soluton / nontrivial solution에 따라 나오게 되는 벡터 간의 관계에 대해서 알아보자.
1. 선형 독립(Linearly independent) / 선형 종속(Linearly dependent)
1.1. 선형 독립(Linearly independent)
- 다음과 같은 선형 방정식(Linear Equation)이 주어져 있다고 생각해보자.
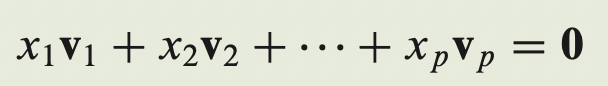
- 해당 방정식이 trivial solution을 가질 때,
--> v1,v2,...vp는 선형 독립(Linearly independent)라고 한다.
1.2. 선형 종속(Linearly dependent)
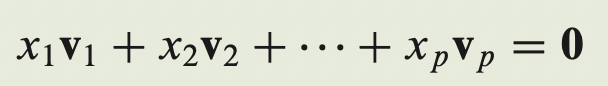
- 해당 방정식이 nontirivial solution을 가질 때,
--> v1,v2,...,vp는 선형 종속(linearly dependent)라고 한다.
1.3. 선형 독립, 선형 종속의 의미
- 선형독립(Linearly independent)와 선형 종속(linearly dependent)에 대해서 알아보았으니
- 각각이 어떤 의미를 가지는 지 살펴보자.
- 이를 이해하기 위해 다음 문제를 함께 풀어보자.

a. 같은 경우 2*v1. = v2 가 되기 때문에 선형종속(linearly dependent)하다고 할 수 있지만,
b. 같은 경우 v1의 실수배론 v2를 만들어 낼 수 없기 때문에 선형독립(linearly independent) 하다고 할 수 있다.
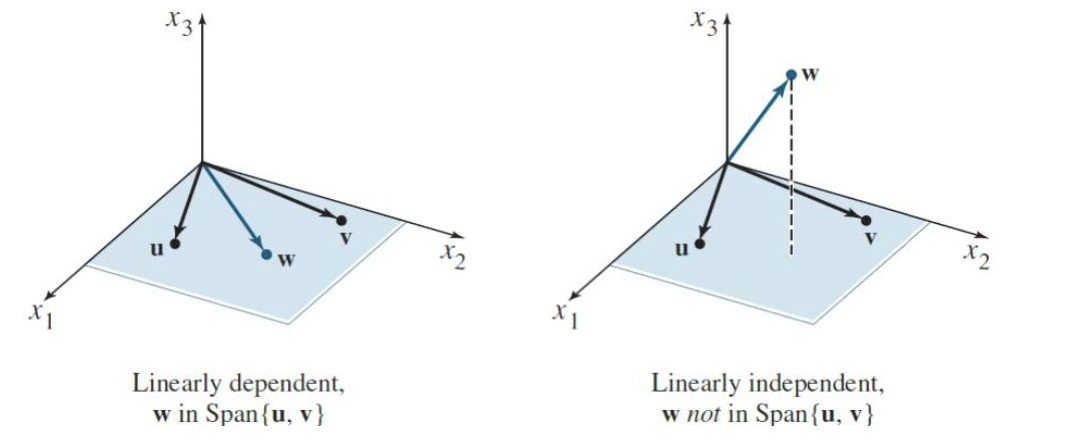
- 이렇듯 선형종속(linearly dependent)하다는 의미는 {a,b,c,..} 이렇게 벡터가 주어져 있을 때,
- 어느 한 벡터가 나머지 벡터들의 선형 결합(linear combination)으로 나타낼 수 있다면, 선형 종속한다고 하고,
- 만일 선형 결합(linear combination)으로 나타낼 수 없다면 선형독립(linearly independent)하다고 할 수 있다.
- 그림으로 나타내면 다음과 같다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-9] The Matrix of a Linear Transformation (0) | 2024.06.03 |
|---|---|
| [Linear Algebra] [1-8] Introduction to Linear Transformations (2) | 2024.06.03 |
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (0) | 2024.06.01 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-3] Vector Equations (0) | 2024.05.31 |
0. Review
- 1-5 챕터에서 우리는 homogeneous equation 에 대해서 알아 봤고,
- 그 해집합(Solution set)이 오직 영벡터(Zero Vector)만 가질때 trivial solution을 가진다고 한다.
- 반대로 다른 해도 가진다면 그땐 nontirivial solution이라고 하였다.
- 이번 챕터에서는 trivial soluton / nontrivial solution에 따라 나오게 되는 벡터 간의 관계에 대해서 알아보자.
1. 선형 독립(Linearly independent) / 선형 종속(Linearly dependent)
1.1. 선형 독립(Linearly independent)
- 다음과 같은 선형 방정식(Linear Equation)이 주어져 있다고 생각해보자.
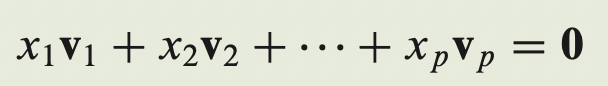
- 해당 방정식이 trivial solution을 가질 때,
--> v1,v2,...vp는 선형 독립(Linearly independent)라고 한다.
1.2. 선형 종속(Linearly dependent)
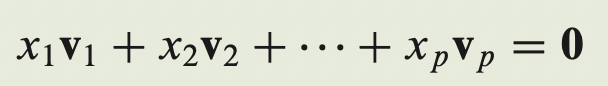
- 해당 방정식이 nontirivial solution을 가질 때,
--> v1,v2,...,vp는 선형 종속(linearly dependent)라고 한다.
1.3. 선형 독립, 선형 종속의 의미
- 선형독립(Linearly independent)와 선형 종속(linearly dependent)에 대해서 알아보았으니
- 각각이 어떤 의미를 가지는 지 살펴보자.
- 이를 이해하기 위해 다음 문제를 함께 풀어보자.

a. 같은 경우 2*v1. = v2 가 되기 때문에 선형종속(linearly dependent)하다고 할 수 있지만,
b. 같은 경우 v1의 실수배론 v2를 만들어 낼 수 없기 때문에 선형독립(linearly independent) 하다고 할 수 있다.
- 이렇듯 선형종속(linearly dependent)하다는 의미는 {a,b,c,..} 이렇게 벡터가 주어져 있을 때,
- 어느 한 벡터가 나머지 벡터들의 선형 결합(linear combination)으로 나타낼 수 있다면, 선형 종속한다고 하고,
- 만일 선형 결합(linear combination)으로 나타낼 수 없다면 선형독립(linearly independent)하다고 할 수 있다.
- 그림으로 나타내면 다음과 같다.

'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-9] The Matrix of a Linear Transformation (0) | 2024.06.03 |
|---|---|
| [Linear Algebra] [1-8] Introduction to Linear Transformations (2) | 2024.06.03 |
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (0) | 2024.06.01 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-3] Vector Equations (0) | 2024.05.31 |

