0. Intro
- 이번 챕터에서는 T(x) = Ax 라고 주어져 있는 행렬변환(Matrix Transformation)에서
- x에 대한 함숫값(image of x) 를 알고 있다면 A를 역추적할 수 있는 방법에 대해서 이번 챕터에서는 배우게 될 것이다.
1. How to get a A
- x의 함숫값(image of x)이 주어졌을 때 행렬A를 구하는 방법에 대해서 알아가기 위해
- 주어진 문제를 같이 풀어보자.
Q)

A)
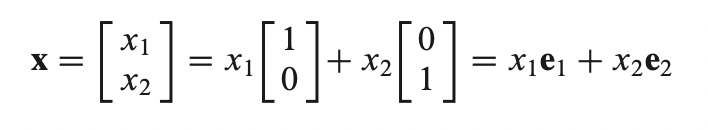
- x벡터를 다음과 같이 나타낼 수 있고 T가 선형결합(linear Transformation)이라고 주어져 있기 때문에
- 다음과 같이 식을 세울수 있다.

-즉 이걸 식변환 해주게 되면 우리가 원하는 A를 구할 수 있다.
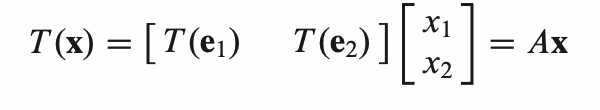
-이걸 정형화 하면 다음과 같다.

- 이를 만족하는 행렬A를 우리는 표준행렬(Standard Matrix) 라고 한다.
2. 회전변환(Rotation Transformation)
- 다음 처럼 어떤 벡터를 pi만큼 회전할 때의 회전 변환(Rotation Transformation)의 Matrix를 구하고 싶다면 다음과 같다.
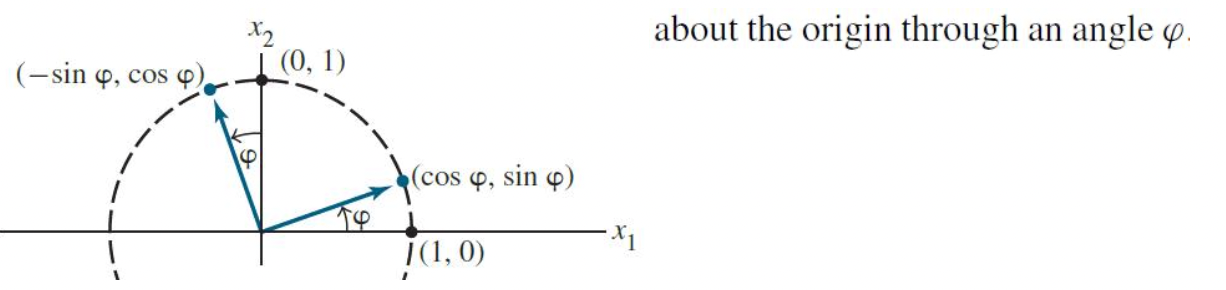
-> T(e1) = (cos pi , sin pi) , T(e2) = (-sin pi, cos pi)
즉 A = [T(e1) T(e2)]
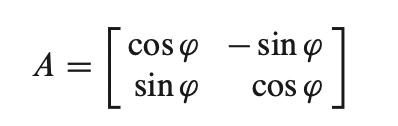
3. onto / one-to-one
3.1. Onto
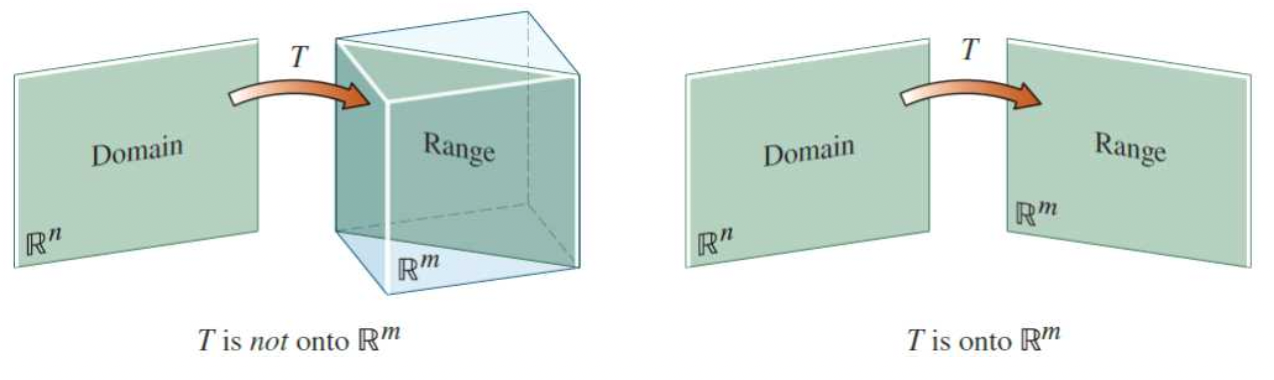
- Onto의 의미는 공역(Codomain)과 치역(Range)가 같은 경우를 뜻한다.
- 선형대수학의 변환(Transformation)에서의 Onto의 의미는 다음과 같다.
T: R^n -> R^m 일때 T의 치역(range)가 모두 codomain R^m과 일치할 때,
onto라고 한다.
3.2. One-to-one
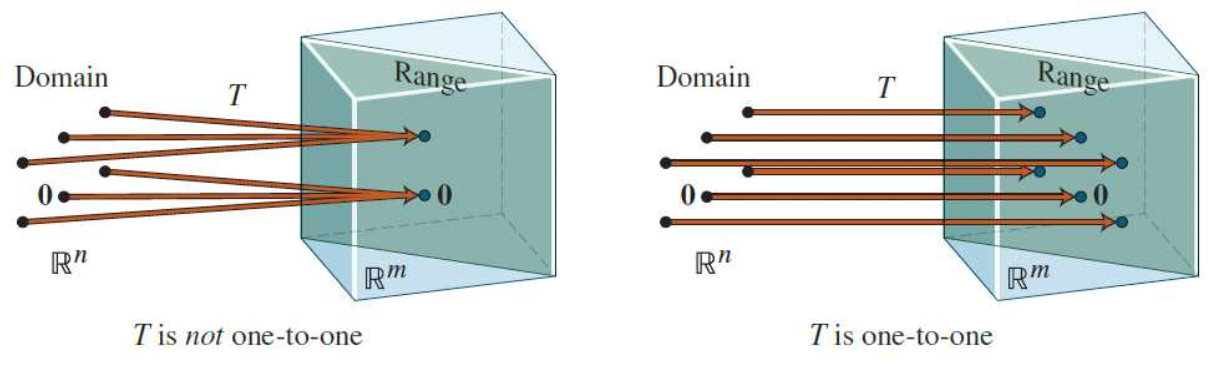
- One-to-One은 우리가 알고 있는 일대일함수와 의미가 동일하다고 생각해도 된다.
- 즉 x1 과 x2가 다르다면 f(x1) 과 f(x2)가 다른것을 의미한다.
- 즉 다음 그림과 같다.
3.3. Onto/One-to-one의 성질
- Onto, One-to-one에 대한 기본적인 의미에 대해서 알았으니
- 어떤 성질을 가지고 있는지 알아보자.
i) Onto
- T가 R^n -> R^m 으로 보내는 선형 변환(linear Transformation)라고 주어져 있고,
- A를 표준행렬(Standard Matrix)라고 해보자.
- T가 Onto일 때 다음과 같은 성질을 갖는다
- Span{columns of A} = R^m 을 만족한다.
ii) One-to-one
- T가 R^n -> R^m 으로 보내는 선형 변환(linear Transformation)라고 주어져 있고,
- A를 표준행렬(Standard Matrix)라고 해보자.
- T가 One-to-one일 때 다음과 같은 성질을 갖는다.
- T(x) = 0 은 오직 trivial solution 만 갖는다.
- columns of A는 선형독립(linearly independent)이다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |
|---|---|
| [Linear Algebra] [2-1] Matrix Operations (0) | 2024.06.03 |
| [Linear Algebra] [1-8] Introduction to Linear Transformations (2) | 2024.06.03 |
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (0) | 2024.06.01 |
0. Intro
- 이번 챕터에서는 T(x) = Ax 라고 주어져 있는 행렬변환(Matrix Transformation)에서
- x에 대한 함숫값(image of x) 를 알고 있다면 A를 역추적할 수 있는 방법에 대해서 이번 챕터에서는 배우게 될 것이다.
1. How to get a A
- x의 함숫값(image of x)이 주어졌을 때 행렬A를 구하는 방법에 대해서 알아가기 위해
- 주어진 문제를 같이 풀어보자.
Q)

A)
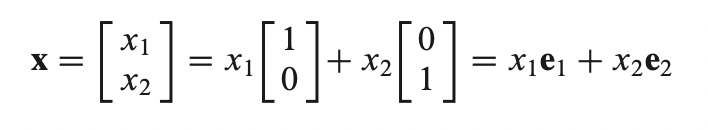
- x벡터를 다음과 같이 나타낼 수 있고 T가 선형결합(linear Transformation)이라고 주어져 있기 때문에
- 다음과 같이 식을 세울수 있다.

-즉 이걸 식변환 해주게 되면 우리가 원하는 A를 구할 수 있다.
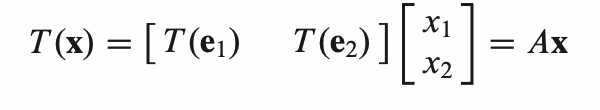
-이걸 정형화 하면 다음과 같다.

- 이를 만족하는 행렬A를 우리는 표준행렬(Standard Matrix) 라고 한다.
2. 회전변환(Rotation Transformation)
- 다음 처럼 어떤 벡터를 pi만큼 회전할 때의 회전 변환(Rotation Transformation)의 Matrix를 구하고 싶다면 다음과 같다.
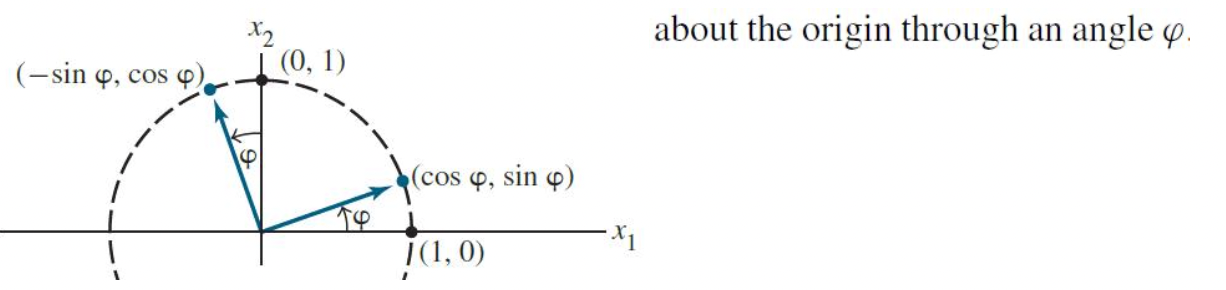
-> T(e1) = (cos pi , sin pi) , T(e2) = (-sin pi, cos pi)
즉 A = [T(e1) T(e2)]
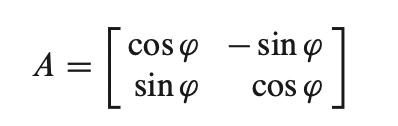
3. onto / one-to-one
3.1. Onto
- Onto의 의미는 공역(Codomain)과 치역(Range)가 같은 경우를 뜻한다.
- 선형대수학의 변환(Transformation)에서의 Onto의 의미는 다음과 같다.
T: R^n -> R^m 일때 T의 치역(range)가 모두 codomain R^m과 일치할 때,
onto라고 한다.

3.2. One-to-one
- One-to-One은 우리가 알고 있는 일대일함수와 의미가 동일하다고 생각해도 된다.
- 즉 x1 과 x2가 다르다면 f(x1) 과 f(x2)가 다른것을 의미한다.
- 즉 다음 그림과 같다.

3.3. Onto/One-to-one의 성질
- Onto, One-to-one에 대한 기본적인 의미에 대해서 알았으니
- 어떤 성질을 가지고 있는지 알아보자.
i) Onto
- T가 R^n -> R^m 으로 보내는 선형 변환(linear Transformation)라고 주어져 있고,
- A를 표준행렬(Standard Matrix)라고 해보자.
- T가 Onto일 때 다음과 같은 성질을 갖는다
- Span{columns of A} = R^m 을 만족한다.
ii) One-to-one
- T가 R^n -> R^m 으로 보내는 선형 변환(linear Transformation)라고 주어져 있고,
- A를 표준행렬(Standard Matrix)라고 해보자.
- T가 One-to-one일 때 다음과 같은 성질을 갖는다.
- T(x) = 0 은 오직 trivial solution 만 갖는다.
- columns of A는 선형독립(linearly independent)이다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |
|---|---|
| [Linear Algebra] [2-1] Matrix Operations (0) | 2024.06.03 |
| [Linear Algebra] [1-8] Introduction to Linear Transformations (2) | 2024.06.03 |
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (0) | 2024.06.01 |

