0. Intro
- 행렬분해(Matrix Factorization)이란 어떤 행렬을 두개 이상의 행렬의 곱(product)로 나타내는 것을 의미한다.
- 이번 챕터에서는 LU Factorization(LU 분해)에 대해서 배워볼 것이다.
1.LU 분해(LU Factorization)
- 어느 m x n 행렬 A의 LU분해라는 것은 A = LU 로 분해하는 것을 의미한다.
- L은 m x m 하삼각행렬(lower triangular matrix), L의 주대각성분은 모두 1, invertible함
- U는 A의 echelon form 즉 A의 REF를 의미함
- L은 invertible 한 행렬이기 때문에 다음과 같은 식을 만족함(해당 식이 만족한다는 걸 잘기억해놓자!)
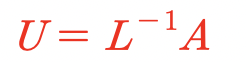
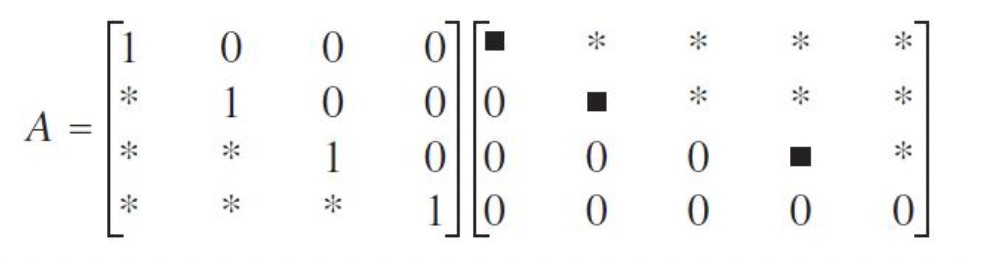
ex) A = LU 꼴은 다음과 같음
2. LU Factorization을 이용하여 해(Solution)찾기
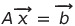
- 라고 주어져 있는 행렬방정식(Matrix Equation)이 있다.
- A라는 행렬을 LU Factorization을 이용하여 A =LU로 분해해보자.
- 그러면 다음과 같은 수식이 만족한다.


- 즉 구하고자 하는 해를 구하기 위해선
- Ly = b에서 y를 먼저 구하고
- Ux= y에서 x를 구하면 된다.
- 확실하게 이해하기 위해 다음과 같은 예제를 확인해보자
ex)



- 기존에 알고 있던 RREF를 만들어서 Solution을 만들 때 row operation의 최소 횟수는 62번이다.
- 하지만 LU Factiorization을 이용해서 구한다면 28번의 row operation이 이용된다.
--> 이렇듯 더욱 효율적이라고 할 수 있다.
3. LU Factorization Algorithm
- LU Factorization을 통해 해를 구하는 방법이 되게 효율적이라는 것을 앞의 스텝에서 알게 되었다.
- 이번 스텝에서는 행렬 A를 LU 행렬곱으로 분해하는 알고리즘에 대해서 배워볼 것이다.
- 행렬 U : 행렬 A에 row replacement만 해서 얻은 REF라고 약속하자.

- 우리는 해당식을 역행렬을 이용해서 L 행렬을 다음과 같이 구할 수 있다.
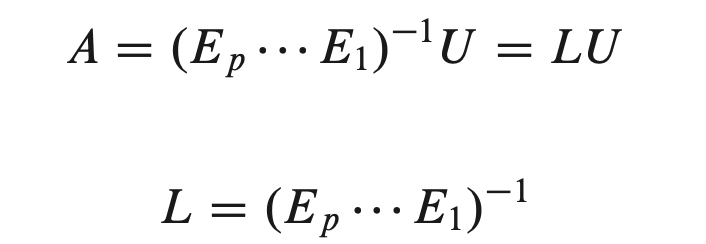
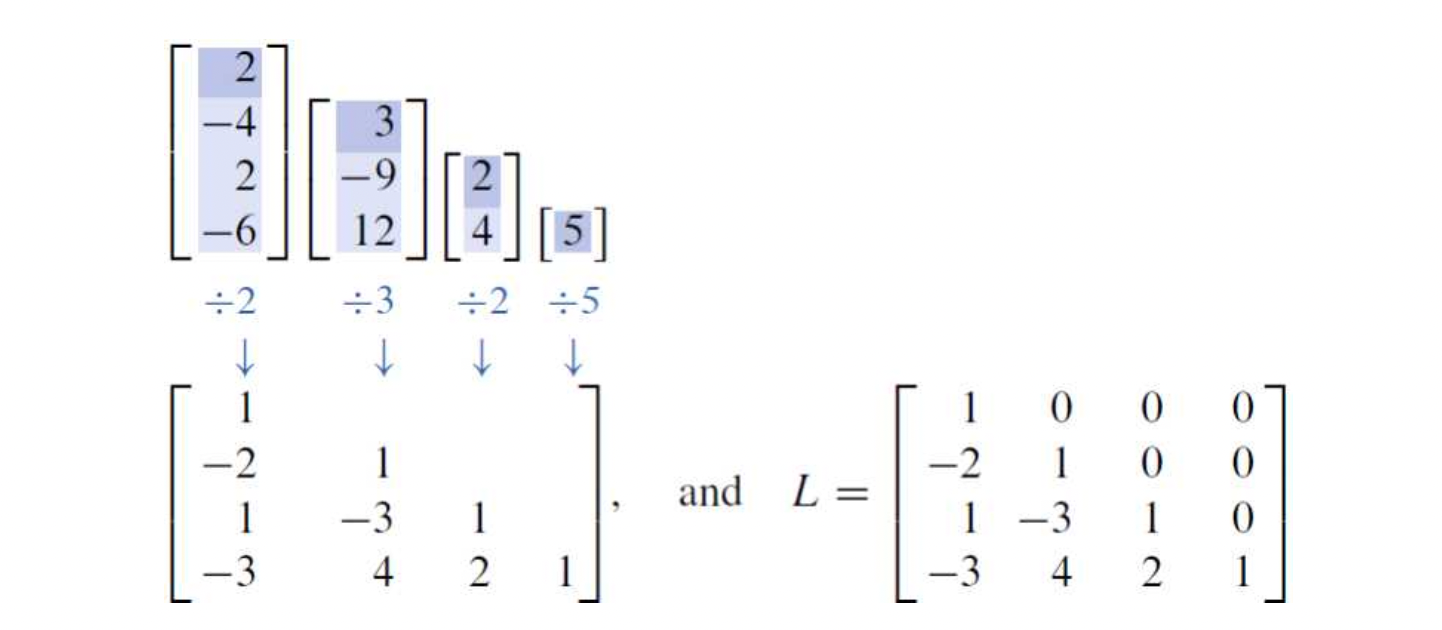
- 예제를 같이 풀어보면서 LU Factorization에 대한 내용을 전체적으로 잡아보자!
ex)


'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-9] Dimension and Rank (2) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-8] Subspaces of R^n (0) | 2024.06.04 |
| [Linear Algebra] [2-4] Partitioned Matrices (1) | 2024.06.04 |
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (4) | 2024.06.03 |
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |

