0. Intro
- 2.2 챕터에서 역행렬(Invertible Matrix)에 대한 기본개념에 대해서 알아보았고
- 이번 챕터에선 그 역행렬이 어떤 성질을 가지고 있는지 알아가보도록 하자.
1. 역행렬정리(The Invertible Matrix Theorem)
- A를 n x n 정방행렬이라고 가정하자.
- 그러면 다음 a부터 l까지의 내용이 전부 참이거나 전부 거짓이 된다.
a. A는 역행렬을 가진다.(Invertible Matrix)
b. A와 In 은 행 상등(row equivalent)하다.
c. A는 n개의 pivot positions을 갖는다.
d. Ax = 0 은 오직 trivial solution뿐이다. (One-to-One)이다.
e. A의 칼럼들은 전부 선형독립(linearly independent)이다
f. T(x) = Ax 는 one-to-one이다.
g. Ax = b를 만족하는 x의 값은 오직 하나이다.
h. Span{Col A} = R^n
i. T(x) = Ax R^n을 R^n으로 보내는 onto 이다.
j. CA = I 를 만족하는 C를 갖는다.
k. AD = I를 만족하는 D를 갖는다.
l. A^{T}는 invertible하다.
2. 역선형변환(Invertible Linear Transformations)
- 다음 조건을 만족하는 S, T가 있다고 생각해보자.
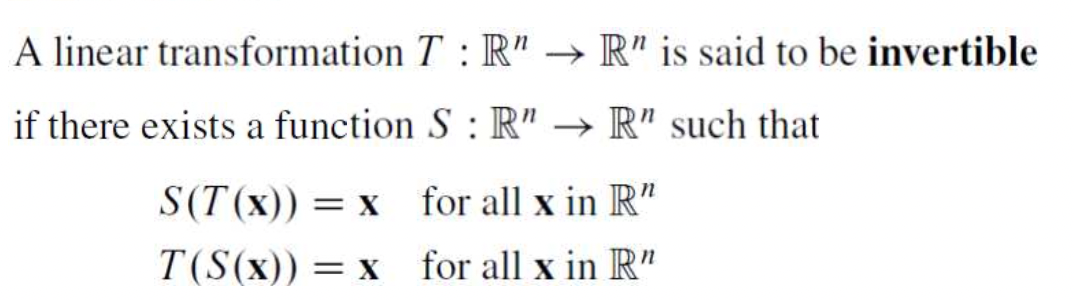
-이때,S는 T의inverse라고 한다.
- 즉, S = T^(-1)이다.
- 만약 A가 T의 standard matrix 라면 A^(-1)은 S의 Standard matrix가 된다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-5] Matrix Factorizations (1) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-4] Partitioned Matrices (2) | 2024.06.04 |
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |
| [Linear Algebra] [2-1] Matrix Operations (0) | 2024.06.03 |
| [Linear Algebra] [1-9] The Matrix of a Linear Transformation (0) | 2024.06.03 |

