0. Intro
- 어떠한 행렬을 columns vector들로 나타냈던것처럼
- 사이즈가 큰 행렬을 행렬들로 나타내는 챕터라고 생각하면 편하다.
- 이렇게 말하면 이해하기 어려울테니 다음 스텝을 한번 봐보자
1. 분할 행렬(Partitioned Matrix)
- 행렬 A가 다음과 같이 주어져 있을때 다음처럼 행렬로 분해하는 걸 Partitioned(block) matrix 라고한다.
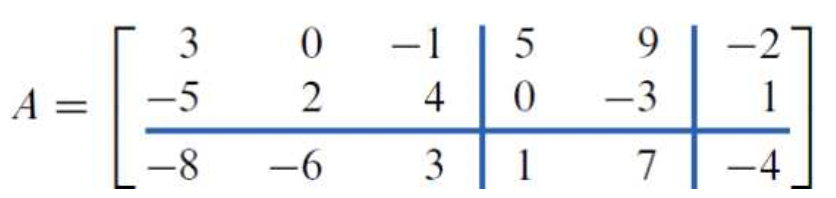
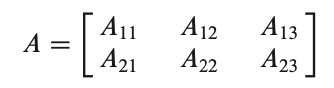
- 각각의 행렬을 submatrix 라고 한다.
ex)

2. Addition and Salar Multiplication
- 기존의 행렬 합 , 스칼라 곱과 마찬가지로 분할 행렬(partitioned Matrix)도 마찬가지로 사이즈가 같다면 행렬 합이 가능하다.
- Scalar Multiplication도 마찬가지 이다.
3. 분할 행렬 곱(Multiplication of Partitioned Matrices)
- 다음과 같이 곱셈도 가능하다. (일반적인 행렬 곱처럼)
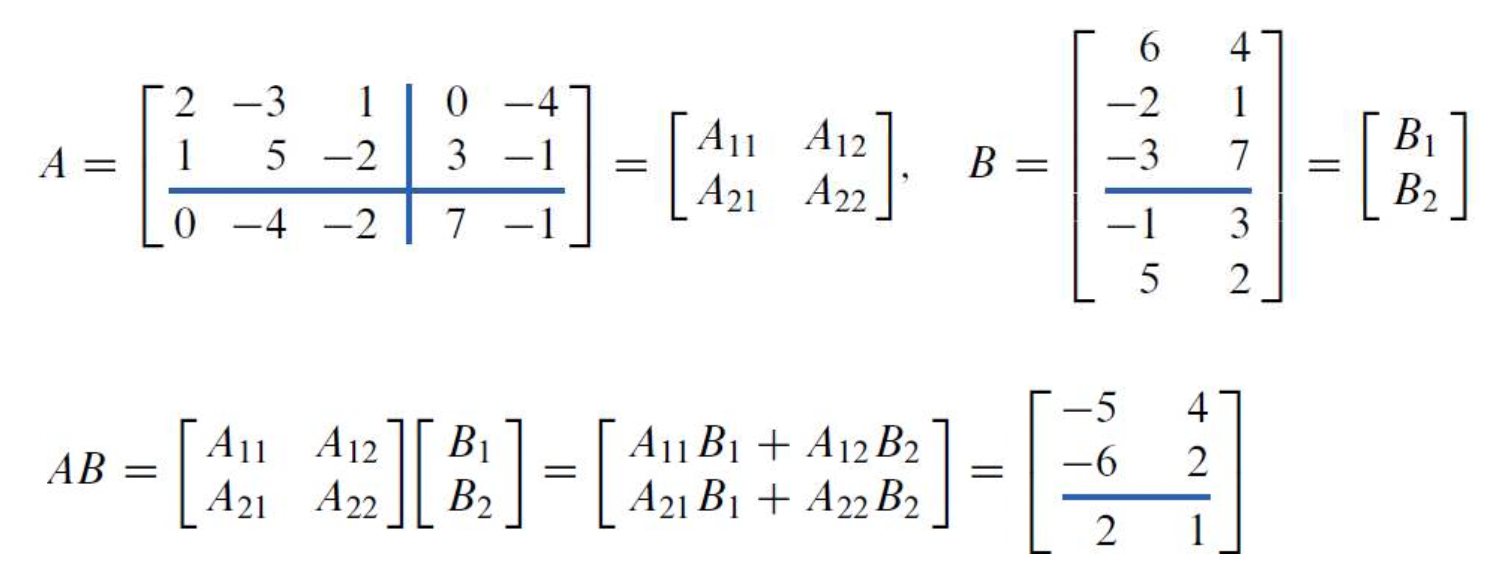
-이번 챕터에서는 그냥 사이즈가 큰 행렬을 submatrix로 나눠서 그 행렬을 하나하나 원소로 생각하는 시선을 만들어주는 챕터이다.
- 그냥 가볍게 가볍게 봐도 이해하기 쉬운 챕터라고 생각한다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-8] Subspaces of R^n (0) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-5] Matrix Factorizations (1) | 2024.06.04 |
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (5) | 2024.06.03 |
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |
| [Linear Algebra] [2-1] Matrix Operations (0) | 2024.06.03 |

