0. Review
- 우리는 2-8에서 basis에 대한 내용을 알아보았다.
- 이번 챕터에서는 basis에 대한 심화적인 개념에 대해서 알아갈까 한다.
1. 좌표 체계(Coordinate System)
- H를 vector space, B = {v1,v2,...,vp}를 H의 basis라고 하자.
그러면 각각 H에 속하는 원소들은 B에 속한 벡터들의 일차결합(Linear combination)으로 unique하게 표현된다.
- 집합 B를 다음과 같이 정의해보자.
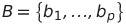
- B를 subspace H의 basis라고 하자.
- 만약 H에 속하는 x가 있다면
- 그 x를 B에 대한 원소에 대한 선형결합(linear combination)으로 나타낼 수 있다.

- 이를 b1,b2...bp를 좌표평면의 축으로 봐서 좌표로 나타낼 수 있다.
ex)
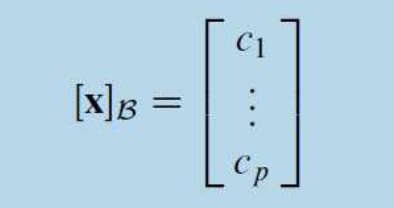
- 이를 B-coordinate vector of x(x의 B에 의한 좌표) 라고 한다.
ex)
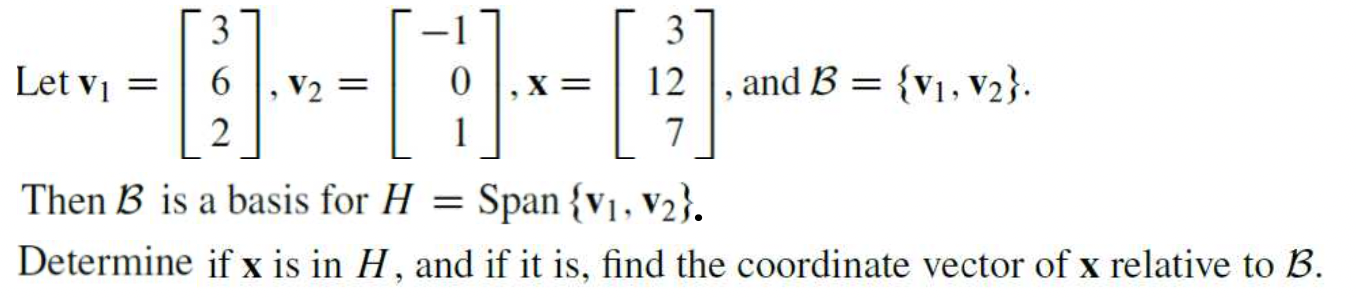
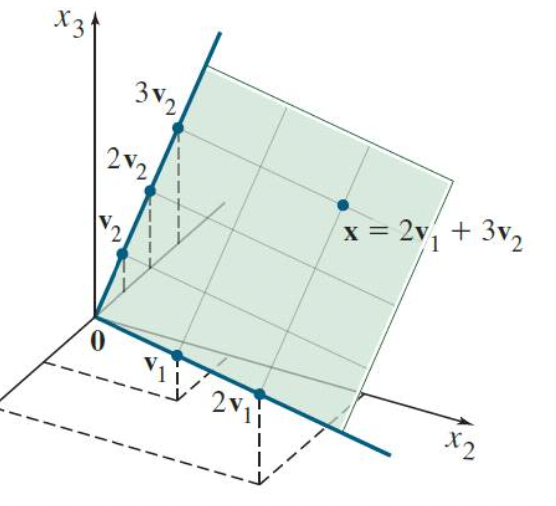
2. The Dimension of a Subspace
- 어떤 Subspace H의 차원(Dimension)을 나타낼 때 다음 처럼 dim(H)로 나타낼 수 있다.
- dim(H)는 H의 basis의 벡터의 개수를 의미한다.
- dim({0}) = 0 이라고 약속하자.
3. Rank
- rank(A) = dim(Col(A)) 과 같다.
- nullity(A) = dim(Nul(A)) 와 같다.
3.1. The Rank Theorem
A가 만약 n개의 columns를 가지고 있다면 다음과 같은 정리를 만족한다.
- Rank(A) + Nullity(A) = n
cf) Rank and the Invertible Matrix Theorem

- 이번 챕터에서 배운 내용이 Invertible Matrix 정리를 더 심화시켜준다
m. 각 A의 칼럼은 R^n의 basis가 된다.
n : Col A = R^n
o. rank A = n
p. Nullity A = 0
q. Nul A = {0}
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-8] Subspaces of R^n (0) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-5] Matrix Factorizations (1) | 2024.06.04 |
| [Linear Algebra] [2-4] Partitioned Matrices (1) | 2024.06.04 |
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (4) | 2024.06.03 |
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |
0. Review
- 우리는 2-8에서 basis에 대한 내용을 알아보았다.
- 이번 챕터에서는 basis에 대한 심화적인 개념에 대해서 알아갈까 한다.
1. 좌표 체계(Coordinate System)
- H를 vector space, B = {v1,v2,...,vp}를 H의 basis라고 하자.
그러면 각각 H에 속하는 원소들은 B에 속한 벡터들의 일차결합(Linear combination)으로 unique하게 표현된다.
- 집합 B를 다음과 같이 정의해보자.
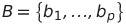
- B를 subspace H의 basis라고 하자.
- 만약 H에 속하는 x가 있다면
- 그 x를 B에 대한 원소에 대한 선형결합(linear combination)으로 나타낼 수 있다.

- 이를 b1,b2...bp를 좌표평면의 축으로 봐서 좌표로 나타낼 수 있다.
ex)
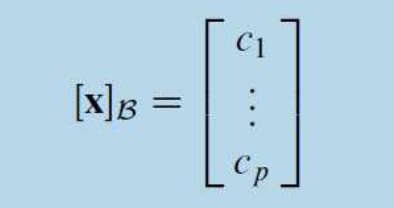
- 이를 B-coordinate vector of x(x의 B에 의한 좌표) 라고 한다.
ex)
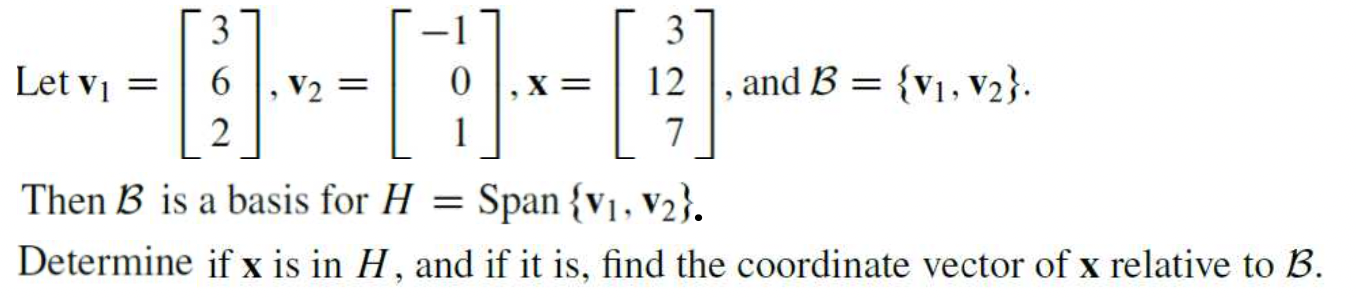

2. The Dimension of a Subspace
- 어떤 Subspace H의 차원(Dimension)을 나타낼 때 다음 처럼 dim(H)로 나타낼 수 있다.
- dim(H)는 H의 basis의 벡터의 개수를 의미한다.
- dim({0}) = 0 이라고 약속하자.
3. Rank
- rank(A) = dim(Col(A)) 과 같다.
- nullity(A) = dim(Nul(A)) 와 같다.
3.1. The Rank Theorem
A가 만약 n개의 columns를 가지고 있다면 다음과 같은 정리를 만족한다.
- Rank(A) + Nullity(A) = n
cf) Rank and the Invertible Matrix Theorem

- 이번 챕터에서 배운 내용이 Invertible Matrix 정리를 더 심화시켜준다
m. 각 A의 칼럼은 R^n의 basis가 된다.
n : Col A = R^n
o. rank A = n
p. Nullity A = 0
q. Nul A = {0}
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-8] Subspaces of R^n (0) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-5] Matrix Factorizations (1) | 2024.06.04 |
| [Linear Algebra] [2-4] Partitioned Matrices (1) | 2024.06.04 |
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (4) | 2024.06.03 |
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |

