1. 부분 공간(Subspace)
- 부분 공간(Subspace)는 다음과 같은 특정한 조건을 만족하는 집합을 의미한다.
- 그 조건은 다음과 같이 3가지이다.
a. 영벡터(zero vector)가 포함되어야 한다.
b. 부분공간(Subspace)에 속하는 벡터 u,v가 있을 때 u+v가 부분공간(Subspace)에 속해야 한다.
c. 부분공간(Subspace)에 속하는 벡터 u가 있을 때 어떤 스칼라 c를 곱한 cu 가 부분공간(Subspace)에 속해야 한다.
- 다음 예제는 Subspace가 아닌 집합이다.

2. Column Space
- Column Space란 어떤 행렬의 칼럼들을 Linear combination으로 나타낼 수 있는 모든원소들의 집합을 의미한다.
- 즉 Column Space 는 Span{어떤 행렬의 칼럼들}을 의미한다.
- Column Space를 줄여서 우리는 Col(A)로 나타낸다.
즉, 다음과 같은 식을 만족한다.
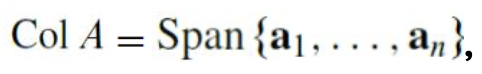
3. Null Space
- Null Space란 homogeneous equation Ax = 0을 만족하는 모든 해집합(Solution set)을 의미한다.

4. Basis for a Subspace
- 어떤 Subspace H의 basis라는 뜻은
- 집합에 있는 원소들이 전부 선형독립(Linearly independent)하고,
- H = Span{basis} 를 만족한다는 것이다.
4.1. Pivot Columns of A 는 basis of Col A와 같다.
- 중요한 성질중 하나는 Pivot Columns of A는 Col A의 basis이다.
- 이를 잘 기억해보자.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-9] Dimension and Rank (2) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-5] Matrix Factorizations (1) | 2024.06.04 |
| [Linear Algebra] [2-4] Partitioned Matrices (2) | 2024.06.04 |
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (5) | 2024.06.03 |
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |

