-
0. 선형대수란(Linear Algebra)?
-
1. 선형방정식(Linear Equations)?
-
2. 일차 연립 방정식(A system of linear equations)?
-
2.1. 선형 연립 방정식의 의미
-
3. 행렬 표기법 (Matrix Notation)
-
3.1. 행렬(Matrix)?
-
3.2. 계수 행렬(Coefficient matrix) / 증강 행렬(Augmented Matrix)
-
4. Solving a Linear System
-
4.1. 기본 행연산(Elementary row operations)
-
4.2. 행 상등(Row equivalent)
0. 선형대수란(Linear Algebra)?
- 선형대수(Linear algebra)는 선형 방정식(Linear equations)를 풀기 위한 방법론이다.
1. 선형방정식(Linear Equations)?
- 선형방정식(Linear Equtions)를 조금 더 직관적으로 이해하기 쉽게 용어를 바꿔준다면
- 일차방정식 이라고 생각하면 편하다. 즉, 변수(variables)들의 차수가 1인 방정식이다.

- x1, x2, ... xn 까지는 변수(Variable) 이라고 하고
- 변수 앞에 붙은 각각의 a1, a2,...an 은 계수(coefficient) 라고 한다.
2. 일차 연립 방정식(A system of linear equations)?
- 일차 연립 방정식(linear system)이란
- 하나 이상의 선형방정식(Linear Equations)의 모음 이다.
ex)
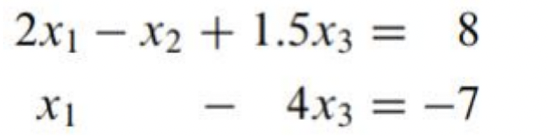
- 일차 연립 방정식(linear system)의 해(Solution)는
- 연립 방정식(System)이 참(Ture)이 되도록 하는 x1,x2...xn 들의 집합을 의미한다.
2.1. 선형 연립 방정식의 의미
- 선형 연립 방정식(Linear sysyem)을 한번 기하적으로 접근해보자.
- 다음과 같은 선형 연립방정식이 주어져 있다.

- 이를 x1,x2 평면위에 나타내 보면 다음과 같은 그래프가 그려진다.
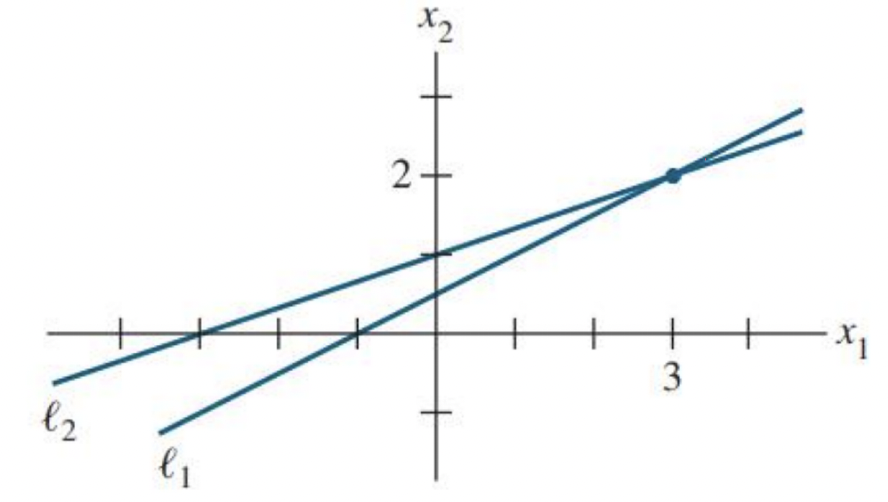
- 즉, 우리가 선형 연립 방정식(Linear System) 의 해(Solution)을 구한다는 것은
- 선형 연립 방정식(Linear System)을 이루고 있는 각각의 선형방정식(Linear equation)의 공통된 교점(intersection point)을 구하는 것과 같다.
- 이러한 기하적인 관점을 토대로 선형 연립 방정식(Linear System)이 해(Solution)를 갖는 유형 3가지에 대해 알아보자.
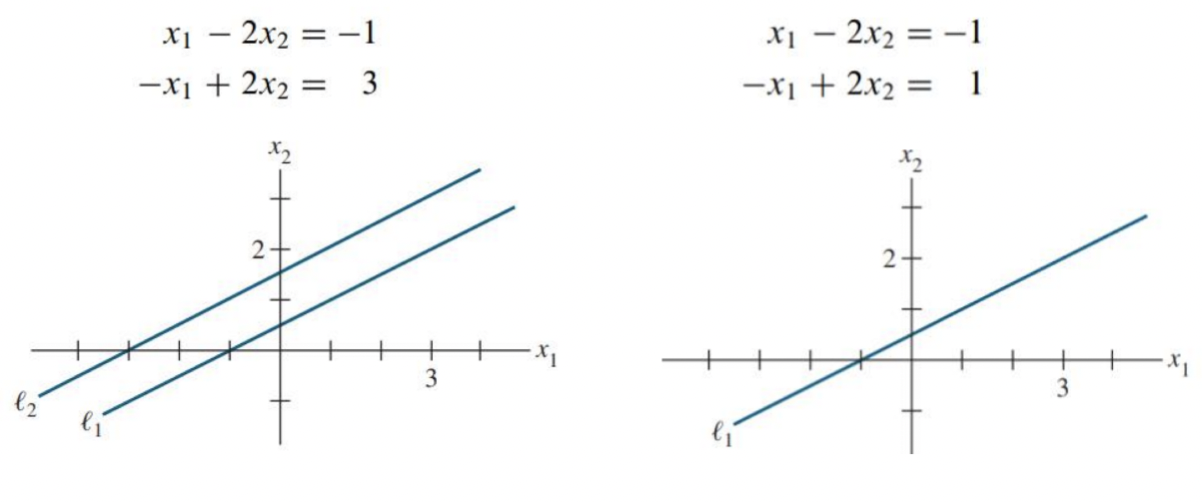
- 우리는 바로 직전에 한 교점에서 만나는 경우를 살펴보았고
- 해당 사진에서 왼쪽은 해를 갖지 않을 때, 오른쪽은 해가 무수히 많을때을 의미한다.
- 즉 선형 연립 방정식(Linear System)이 해(Solution)을 갖는 유형 3가지는 다음과 같다.
i) 오직 단 하나의 해를 가질 때 (exactly one solution)
ii) 무수히 많은 해를 가질 때 (infinitely many solutions)
iii) 해를 가지지 않을 때 (no solution)
- i), ii) 일 때 선형 연립 방정식(Linear System)이 해(Solution)을 가지게 되는데,
이를 연립방정식의 해가 존재한다(Consistent) 라고 한다.
-iii) 일 땐 반대로 해(Solution)을 가지지 않게 되는데,
이를 연립방정식의 해는 존재하지 않는다(Inconsistent) 라고 한다.
3. 행렬 표기법 (Matrix Notation)
- 우리는 앞으로 선형 연립 방정식(Linear System)의 해(Solution)을 구할 때
- 선형 연립 방정식(Linear System)을 행렬(Matrix)로 변환한 뒤에 진행할 것이다.
- 우선 행렬(Matrix)에 대해 먼저 알아 보자.
3.1. 행렬(Matrix)?
- 행렬(Matrix)란 1개 이상의 수나 식을 직사각형의 배열로 나열 한 것을 의미한다.

- 가로줄을 행(row), 세로줄을 열(column)이라고 부른다.
- Aij 이란 행렬(Matrix)에서 i번째 행 j번째 열의 원소를 의미한다.
- 행렬의 크기(size)는 [행(row)의 개수] x [열(column)의 개수] 이다.
3.2. 계수 행렬(Coefficient matrix) / 증강 행렬(Augmented Matrix)
- 다음과 같은 연립방정식(System)이 주어져 있다고 생각해보자.
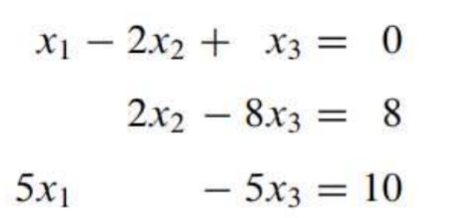
- 해당 선형 연립방정식(Linear System)에 있는 계수(Coefficient)만 따로 빼서 행렬을 만들어보자.
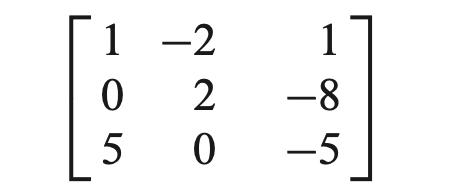
- 이렇듯 선형 연립방정식의 계수만 따로 뺀 행렬을 계수 행렬(Coefficient Matrix) 라고 한다.
- 해당 계수 행렬(Coefficient Matrix)에서 우변에 있는 상수까지 포함하여 행렬을 만들어보자

- 기존의 계수 행렬(Coefficient Matrix) 에서 조금 더 증강된 행렬이 되었기에
- 이를 증강 행렬(Augmented Matrix)라고 한다.
- 우리는 향후 선형 연립방정식(Linear system)의 해집합(Solution Set)을 구할 때
- 주로 증강 행렬(Augmented Matrix)를 이용하여 구할 것이다.
4. Solving a Linear System
- 해당 챕터에서는 선형 연립방정식(Linear system)의 해(solution)을
- 구하기 쉽게 해주는알고리즘(Algorithm)을 설명하고자 한다.
- 즉, 같은 해(Solution)을 가지는 좀 더 풀기 쉬운 연립 방정식(System)으로 만들어 주는 것이다.
- 본격적으로 알아가기 전에 알아야 하는 배경지식 두가지를 알아가보자.
i) 기본 행연산 (Elementary row operations)
ii) 행 상등(Row equivalent)
4.1. 기본 행연산(Elementary row operations)
- 어떤 연립방정식(System)을 좀더 풀기 쉬운 연립 방정식(Syetem)으로 만들어 주기 위해
- 행끼리 연산을 하게 되는데 이를 기본 행연산(Elementary row operation)이라고 한다.
- 기본 행연산(Elementary row operation)은 3가지가 존재한다.
i) Interchange(Swap)
- 행렬에서 두개의 행끼리 교환하는(Interchange) 하는 연산(Operation)을 의미한다.
ex)
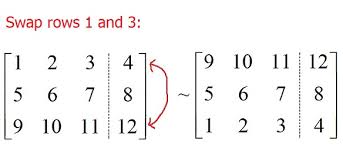
- 다음 예제처럼 1행 과 3행의 위치를 바꿔주는 연산을 Interchange 라고 한다.
(Interchange row1 and row3)
ii) Scaling
- 어느 한 행(row)에 0을 제외한 실수배를 하는 연산이다.
ex) (Scale row3 by k)

iii) Replacement
- 한 개의 열(row)를 그 열(row)과 다른 열(row)의 실수배를 더해준 것으로 대체하는 연산이다.
ex) (Replace row 1 by row1 + k * row2)
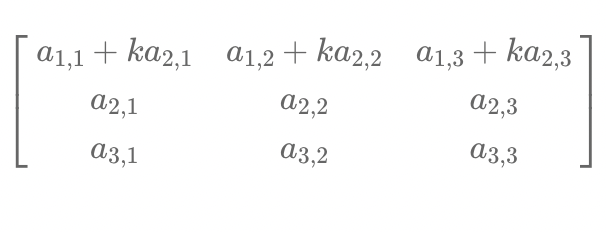
4.2. 행 상등(Row equivalent)
- 어떤 두 행렬이 기본 행 연산(Elementary row operation)을 통해서 만들어 지는 관계라면
- 행 상등(Row equivalent)이라고 한다.
- 두 행렬(Matrix)이 행 상등(Row equivalent)하다면
- 두 연립방정식(systems)는 같은 해 집합(Same solution set)을 갖는다.
- 행 상등(Row Equivalent)가 중요한 이유에 대해 알아보자.
- 만약, 첫 번째 연립방정식(System)의 해 집합(Solution Set)을 구하기 까다롭고
- 두 번째 연립방정식이 첫 번째와 행 상등(row equivalent)하고, 해집합(Solution set)을 구하기 편하다면,
- 두 번째 연립방정식을 풀어 해집합을 구하는 것은 첫 번째 연립방정식의 해집합을 구하는 것과 같다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
|---|---|
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (1) | 2024.06.01 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-3] Vector Equations (0) | 2024.05.31 |
| [Linear Algebra] [1-2] Row reduction & Echelon Forms (0) | 2024.05.31 |
0. 선형대수란(Linear Algebra)?
- 선형대수(Linear algebra)는 선형 방정식(Linear equations)를 풀기 위한 방법론이다.
1. 선형방정식(Linear Equations)?
- 선형방정식(Linear Equtions)를 조금 더 직관적으로 이해하기 쉽게 용어를 바꿔준다면
- 일차방정식 이라고 생각하면 편하다. 즉, 변수(variables)들의 차수가 1인 방정식이다.

- x1, x2, ... xn 까지는 변수(Variable) 이라고 하고
- 변수 앞에 붙은 각각의 a1, a2,...an 은 계수(coefficient) 라고 한다.
2. 일차 연립 방정식(A system of linear equations)?
- 일차 연립 방정식(linear system)이란
- 하나 이상의 선형방정식(Linear Equations)의 모음 이다.
ex)
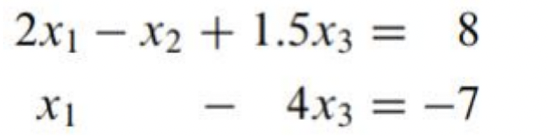
- 일차 연립 방정식(linear system)의 해(Solution)는
- 연립 방정식(System)이 참(Ture)이 되도록 하는 x1,x2...xn 들의 집합을 의미한다.
2.1. 선형 연립 방정식의 의미
- 선형 연립 방정식(Linear sysyem)을 한번 기하적으로 접근해보자.
- 다음과 같은 선형 연립방정식이 주어져 있다.

- 이를 x1,x2 평면위에 나타내 보면 다음과 같은 그래프가 그려진다.

- 즉, 우리가 선형 연립 방정식(Linear System) 의 해(Solution)을 구한다는 것은
- 선형 연립 방정식(Linear System)을 이루고 있는 각각의 선형방정식(Linear equation)의 공통된 교점(intersection point)을 구하는 것과 같다.
- 이러한 기하적인 관점을 토대로 선형 연립 방정식(Linear System)이 해(Solution)를 갖는 유형 3가지에 대해 알아보자.
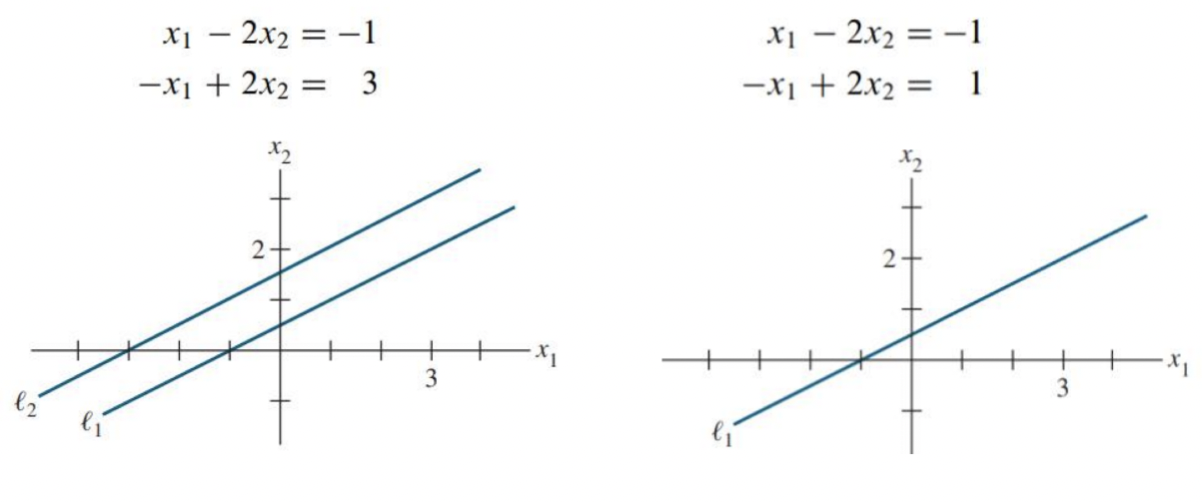
- 우리는 바로 직전에 한 교점에서 만나는 경우를 살펴보았고
- 해당 사진에서 왼쪽은 해를 갖지 않을 때, 오른쪽은 해가 무수히 많을때을 의미한다.
- 즉 선형 연립 방정식(Linear System)이 해(Solution)을 갖는 유형 3가지는 다음과 같다.
i) 오직 단 하나의 해를 가질 때 (exactly one solution)
ii) 무수히 많은 해를 가질 때 (infinitely many solutions)
iii) 해를 가지지 않을 때 (no solution)
- i), ii) 일 때 선형 연립 방정식(Linear System)이 해(Solution)을 가지게 되는데,
이를 연립방정식의 해가 존재한다(Consistent) 라고 한다.
-iii) 일 땐 반대로 해(Solution)을 가지지 않게 되는데,
이를 연립방정식의 해는 존재하지 않는다(Inconsistent) 라고 한다.
3. 행렬 표기법 (Matrix Notation)
- 우리는 앞으로 선형 연립 방정식(Linear System)의 해(Solution)을 구할 때
- 선형 연립 방정식(Linear System)을 행렬(Matrix)로 변환한 뒤에 진행할 것이다.
- 우선 행렬(Matrix)에 대해 먼저 알아 보자.
3.1. 행렬(Matrix)?
- 행렬(Matrix)란 1개 이상의 수나 식을 직사각형의 배열로 나열 한 것을 의미한다.

- 가로줄을 행(row), 세로줄을 열(column)이라고 부른다.
- Aij 이란 행렬(Matrix)에서 i번째 행 j번째 열의 원소를 의미한다.
- 행렬의 크기(size)는 [행(row)의 개수] x [열(column)의 개수] 이다.
3.2. 계수 행렬(Coefficient matrix) / 증강 행렬(Augmented Matrix)
- 다음과 같은 연립방정식(System)이 주어져 있다고 생각해보자.
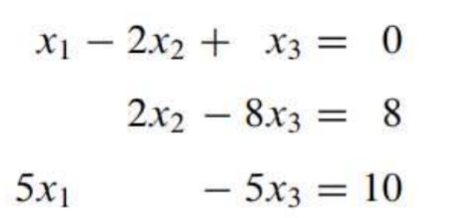
- 해당 선형 연립방정식(Linear System)에 있는 계수(Coefficient)만 따로 빼서 행렬을 만들어보자.
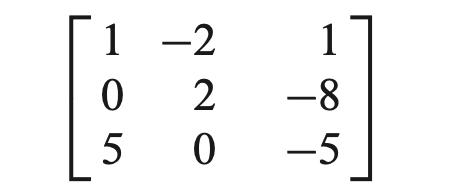
- 이렇듯 선형 연립방정식의 계수만 따로 뺀 행렬을 계수 행렬(Coefficient Matrix) 라고 한다.
- 해당 계수 행렬(Coefficient Matrix)에서 우변에 있는 상수까지 포함하여 행렬을 만들어보자

- 기존의 계수 행렬(Coefficient Matrix) 에서 조금 더 증강된 행렬이 되었기에
- 이를 증강 행렬(Augmented Matrix)라고 한다.
- 우리는 향후 선형 연립방정식(Linear system)의 해집합(Solution Set)을 구할 때
- 주로 증강 행렬(Augmented Matrix)를 이용하여 구할 것이다.
4. Solving a Linear System
- 해당 챕터에서는 선형 연립방정식(Linear system)의 해(solution)을
- 구하기 쉽게 해주는알고리즘(Algorithm)을 설명하고자 한다.
- 즉, 같은 해(Solution)을 가지는 좀 더 풀기 쉬운 연립 방정식(System)으로 만들어 주는 것이다.
- 본격적으로 알아가기 전에 알아야 하는 배경지식 두가지를 알아가보자.
i) 기본 행연산 (Elementary row operations)
ii) 행 상등(Row equivalent)
4.1. 기본 행연산(Elementary row operations)
- 어떤 연립방정식(System)을 좀더 풀기 쉬운 연립 방정식(Syetem)으로 만들어 주기 위해
- 행끼리 연산을 하게 되는데 이를 기본 행연산(Elementary row operation)이라고 한다.
- 기본 행연산(Elementary row operation)은 3가지가 존재한다.
i) Interchange(Swap)
- 행렬에서 두개의 행끼리 교환하는(Interchange) 하는 연산(Operation)을 의미한다.
ex)

- 다음 예제처럼 1행 과 3행의 위치를 바꿔주는 연산을 Interchange 라고 한다.
(Interchange row1 and row3)
ii) Scaling
- 어느 한 행(row)에 0을 제외한 실수배를 하는 연산이다.
ex) (Scale row3 by k)

iii) Replacement
- 한 개의 열(row)를 그 열(row)과 다른 열(row)의 실수배를 더해준 것으로 대체하는 연산이다.
ex) (Replace row 1 by row1 + k * row2)
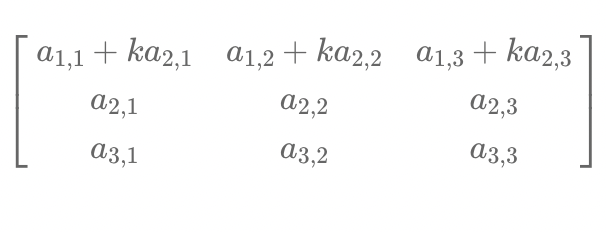
4.2. 행 상등(Row equivalent)
- 어떤 두 행렬이 기본 행 연산(Elementary row operation)을 통해서 만들어 지는 관계라면
- 행 상등(Row equivalent)이라고 한다.
- 두 행렬(Matrix)이 행 상등(Row equivalent)하다면
- 두 연립방정식(systems)는 같은 해 집합(Same solution set)을 갖는다.
- 행 상등(Row Equivalent)가 중요한 이유에 대해 알아보자.
- 만약, 첫 번째 연립방정식(System)의 해 집합(Solution Set)을 구하기 까다롭고
- 두 번째 연립방정식이 첫 번째와 행 상등(row equivalent)하고, 해집합(Solution set)을 구하기 편하다면,
- 두 번째 연립방정식을 풀어 해집합을 구하는 것은 첫 번째 연립방정식의 해집합을 구하는 것과 같다.
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
|---|---|
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (1) | 2024.06.01 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-3] Vector Equations (0) | 2024.05.31 |
| [Linear Algebra] [1-2] Row reduction & Echelon Forms (0) | 2024.05.31 |

