0. Review
- [1-1]챕터에선 어떤 선형 연립방정식(Linear System)을
- 해집합(Solution set)을 구하기 쉬운 형태로 바꿔주는 연산에 대해서 알아갔다.
- 이번 챕터에선 그 형태(Echelon Forms)에 대해서 알아가보자.
1. (사다리꼴행렬)Echelon Forms
- 선형대수학에서 쓰이는 (사다리꼴 행렬)Echelon Forms은 Row Echelon Forms (약어 REF)로 주로 쓰인다.
- 다음 세가지 조건에 만족해야만 REF가 될 수 있다.
1) 모든 원소가 0이 아닌 행(row)은 무조건 모든 원소가 0인 행보다 위에 있어야 한다.
2) 각 행(row)의 Leading Entry는 위의 행(row)보다 열(Column) 기준으로 오른쪽에 위치해야합니다.
cf) Leading Entry 란 행(row)를 읽었을 때 처음으로 0이 아닌 성분을 의미한다.
3) 모든 Leading Entry들의 아래에 존재하는 성분들은 전부 0이여야 한다.
ex)
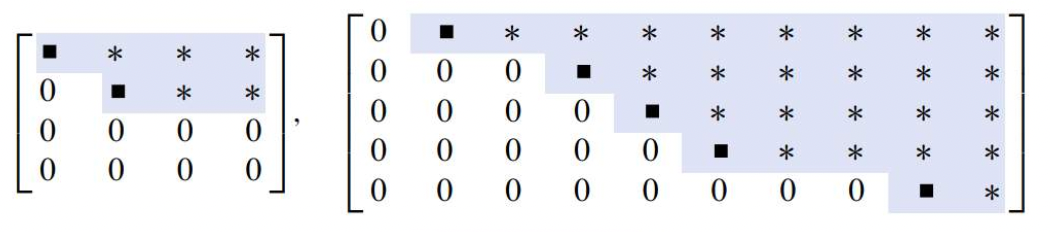
2. Reduced Row Echelon Forms(RREF)
- 기존 REF에서 추가적으로 두가지 조건을 더 만족한다면 RREF가 될 수 있다.
- 그 두가지 조건은 다음과 같다.
4) Leading Entry는 모두 1이다.
5) Leading Entry를 포함하는 열(Columns)에서 Leading Entry를 제외한 모든 열의 성분들은 0이여야 한다.
ex)
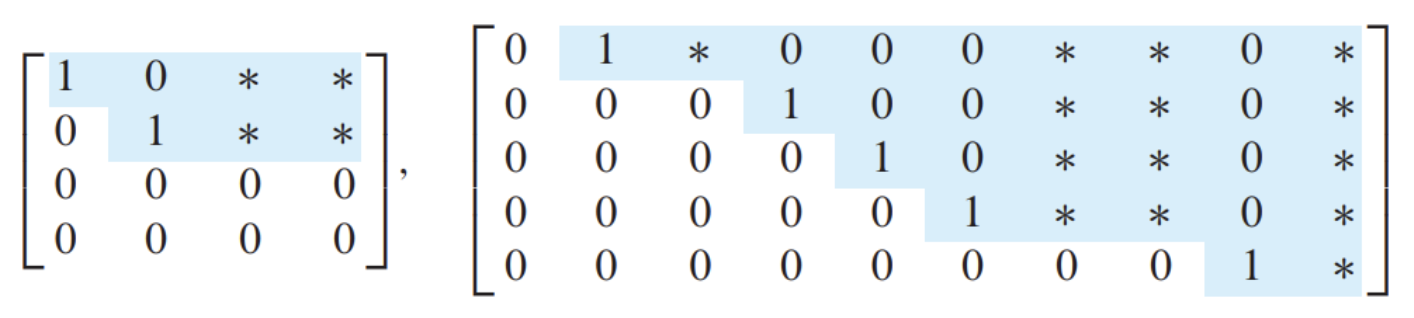
- RREF에서 가장 중요한 특징이 존재한다.
--> 각 행렬은 단 하나의 RREF와 행 상등(Equivalent)하다. / 즉 RREF는 유일성(Uniqueness of the RREF) 을 가진다.
해당 특징에 대해서 왜 그런지 한번 증명을 해보자.
2.1. 유일성 (Uniqueness of the RREF)
- 해당 증명은 Holzmann의 “THE Proof” 을 참고하였다.
정리(Theorem) : 어떤 행렬의 RREF는 유일하다. (Unique)
증명(Proof)
- 어떤 임의의 행렬(Matrix)의 RREF가 두 개의 행렬 R, S가 있다고 가정해보자.
- RREF가 유일함을 보일려면 R = S임을 보여야 한다.
- 만약 R ≠ S라고 가정하자.
- 본격적인 증명에 앞서서 R,S에 대해 각각 다음의 조건에 맞는 행렬 R' ,S'을 추출해보자.
i) R,S에서 가장 첫번째(가장 왼쪽)열을 선택
ii) 선택한 열 왼쪽에 있는 leading 1 columns(Pivot Columns)들을 선택
예를 들면 다음과 같다.
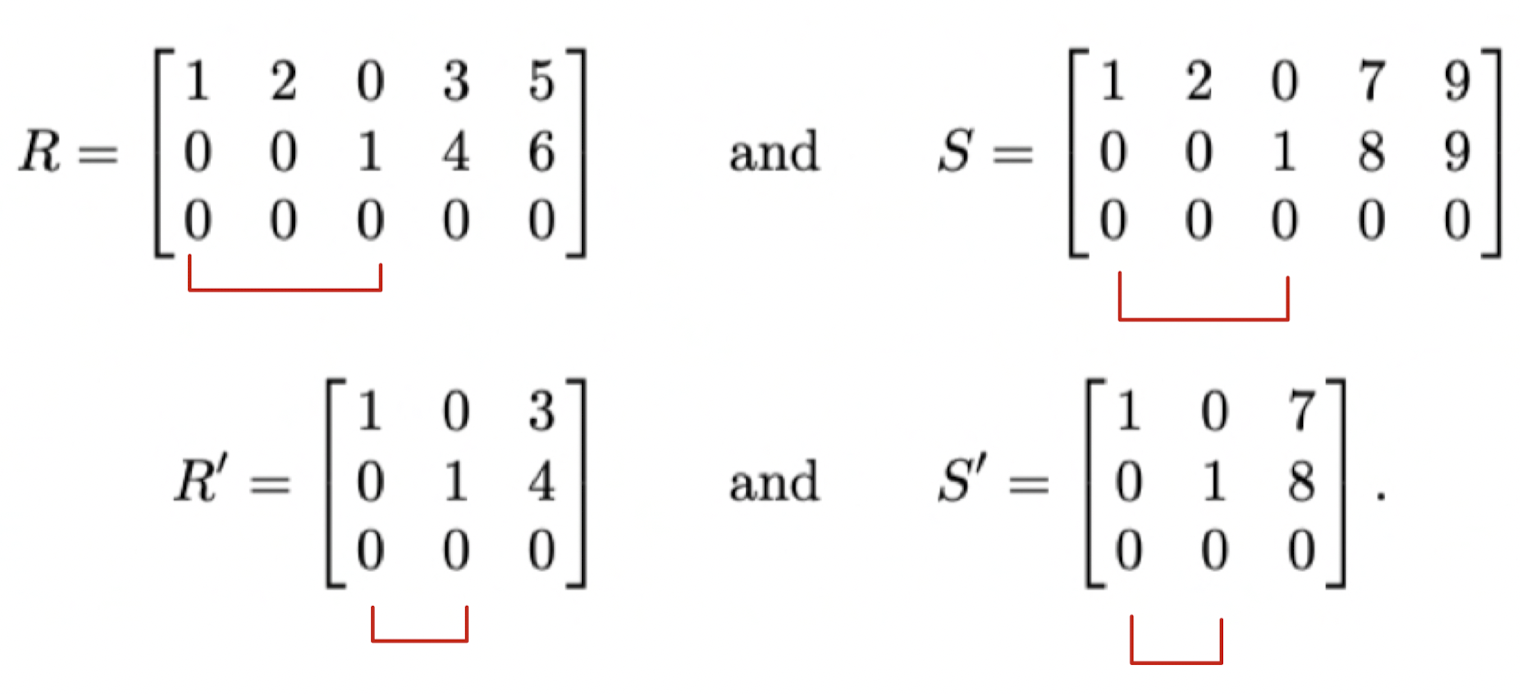
- 이를 일반화해서 다시 한번 나타내보자.

- 열(Row)을 삭제해도 행 상등(Row Equivalent)에는 영향을 미치지 않는다.
- 따라서 R' 과 S' 는 행 상등(Row Equivalent)하다.
- R'과 S'을 강화행렬(Augmented Matrix)라고 해석해보자.
- 그러면 연립방정식 R'(The system of R')은 유일한 해(unique solution) r'을 갖거나 inconsistent하고,
- 연립방정식 S'(The system of S')은 유일한 해(unique soluition) s'을 갖거나 inconsistent하다.
- 처음부터 R 과 S 연립방정식(System)은 상등(Equivalent)하기 때문에,
- r' = s' 이거나 두 R', S'은 inconsistent 라는건 자명하다.
- 따라서 어느 경우든 R' = S' 이기 때문에 모순이다.
- 따라서 어떤 행렬의 RREF는 유일하다.
2.2. Pivot Positions
- 앞서서 2.1. RREF의 유일성에 대해서 증명해보았다.
- 어떠한 행렬의 RREF는 유일하기 때문에 leading entry의 위치는 항상 고정적이다.
- 여기서 leading entry의 위치를 pivot position이라고 한다.
- Pivot position이 속하는 열(columns)을 Pivot Column이라고 부른다.
- Pivot Position, Pivot Column의 개념들은 향후 중요한 역할을 담당하게 되니 잘 정리해보지.
3. The Row Reduction Algorithm(Gauss -Jordan Elimination)
- RREF에 대해서 알아봤으니 RREF를 만들어 가는 알고리즘(algorithm)에 대해 알아보자.
- 그중 행 줄임 알고리즘(Row Reduction Algorithm)에 대해 알아보자.
- Row Reduction 이라고 하기도 하고, 가우스 - 조던 소거법(Gauss -Jordan Elimination)이라고도 불린다.
- 해당 알고리즘은 크게 5가지 단계로 구성되어 있다.
- 1~4단계까지를 전향단계(forward phase), 5단계를 후향단계(backward phase)라고 한다.
- 전형단계에선 REF를 만들어가고, 후향단계에선 REFF를 만들어 간다고 생각하면 된다.
Step 1. 행렬의 가장 왼쪽 위의 pivot position에서 시작된다.
- 만약에 해당 위치의 원소가 0 이라면 다른 행과 interchange 해줘야 한다.

- 1행을 보면 0으로 시작되기 때문에 1행과 3행을 Interchange 해줘서 1로 맞춰줘야 한다.
Step 2. Pivot column에서 pivot으로 0이 아닌 entry를 선택해야된다. 필요하다면 interchange를 한다.
ex) Interchange rows 1 and 3.

Step 3. Replacement 연산을 사용해서 pivot 아래의 원소들을 모두 0으로 만들자.
ex) replace row 2 by row2 - row1

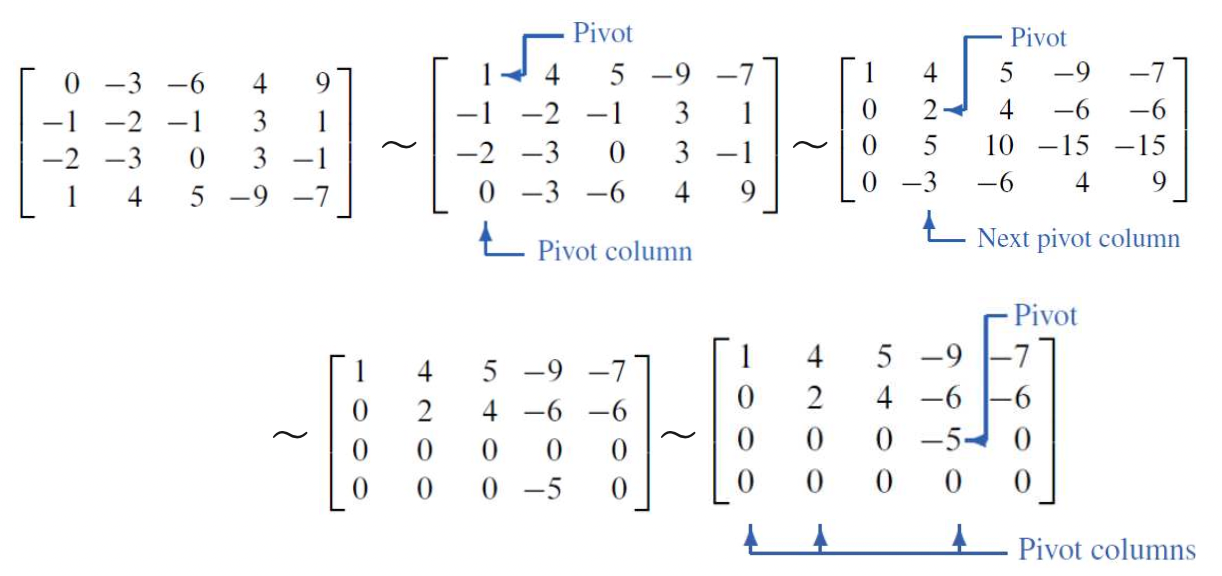
Step 4. 나머지 submatrix들도 1~3과정을 반복하여 적용시켜준다.
--> 1~4 까지의 과정을 마치게 되면 다음과 같은 REF 이 만들어 진다.

Step 5. 가장 오른쪽에 있는 Pivot부터 차례로 해당 pivot이 있는 column위의 원소들을 0으로 만들어준다.
--> Replacement를 이용하여야 함!
- 5단계 까지 적용하게 된다면 RREF를 얻게 된다.

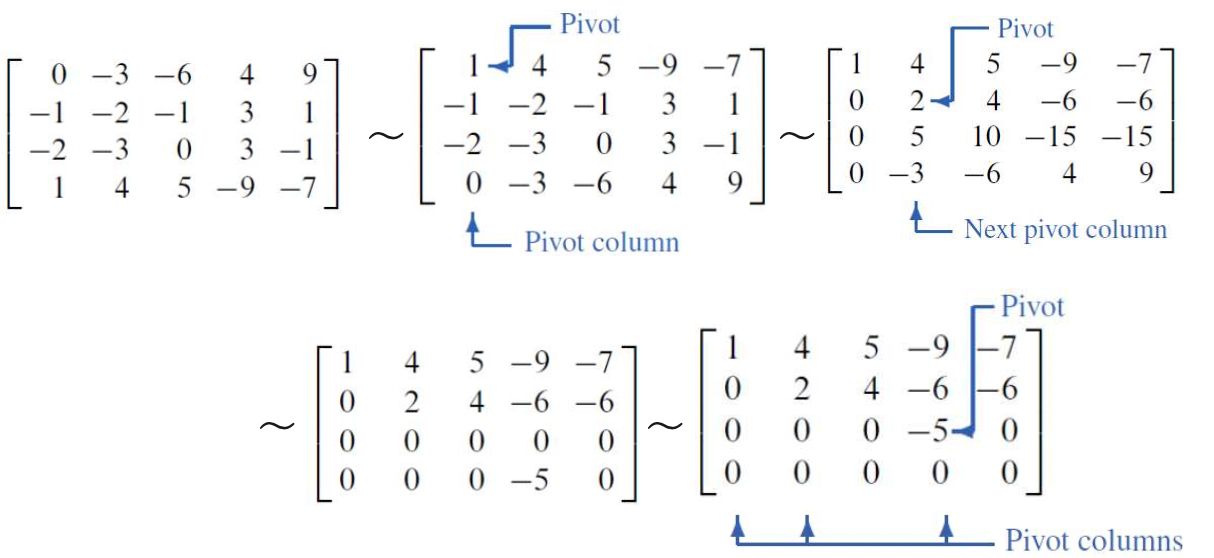
- 1~5단계 까지의 전체적인 과정을 담은 Elemantary row operation의 과정보이면 다음과 같다.
cf) 행렬과 행렬을 이은 ~ 표시는 행 상등(equivalent) 하다는 의미를 가진다.

4. Solutions of Linear Systems
- 증강행렬(Augmented Matrix)를 row reduction algorithm을 통해서 RREF를 만들어 내면
- 해집합(Solution set)에 대한 정보를 알아낼 수 있다.
- 예를들어 REF로 이루어진 증강행렬(Augmented Matrix)가 주어져 있다.

- 증강행렬(Augmented Matrix)의 열(Colunm)의 개수가 4개이기 때문에
- 해당 행렬의 변수의 개수는 3개이다.
- 해당 증강행렬(Augmented Matrix)를 연립방정식(System)으로 표현하면 다음과 같다.

- 우리는 여기서 몇 가지 용어에 대해서 정의를 하고 가볼까한다.
- Pivot Columns 에 있는 변수들 (해당 예제에선 x_{1} , x_{2})는 basic variables 이라고 한다.
- 그리고 나머지 Columns에 있는 변수들(x_{3)은 free variables 라고 한다.
- free variables 의 의미는 값으로 아무(any) 실수나 가져도 되는 변수를 의미한다.
- 해당 연립방정식을 free variable, basic variable을 이용해서 해집합을 나타내면 다음과 같다.

- 여기서 x_{3} is free 라고 나타낸 것은 free variable를 해집합(Solution set)에 나타내 주는 방식이다.
- 다음과 같이 해집합(Solution set)을 나타낸 방식을 General Solution 이라고 한다.
- 만약 증강행렬(Augmented Matrix)를 Row Reduction Algorithm을 통해 RREF로 나타냈을 때
- 다음과 같이 Pivot(leading entry)가 마지막 열(Columns)에 위치하게 된다고 생각해보자.

- 이렇게 되면 마지막 열(row) --> 0 = 1 이라는 모순이 발생하기 때문에
- 해당 연립방정식(System)은 해가 존재하지 않는다(inconsistent)
- 즉 leading entry가 마지막 열(Columns)에 위치한다면
- 연립방정식(System)은 해가 존재하지 않는다(inconsistent)
'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |
|---|---|
| [Linear Algebra] [1-5] Solution Sets of Linear Systems (1) | 2024.06.01 |
| [Linear Algebra] [1-4] The Matrix Equation Ax = b (0) | 2024.06.01 |
| [Linear Algebra] [1-3] Vector Equations (0) | 2024.05.31 |
| [Linear Algebra] [1-1] Systems of Linear equations (0) | 2024.05.30 |

