0. Intro
- Chapter 1 에선 행렬른 다른 벡터로 보내는 함수로 생각하였다.
- 수학에서 함수가 핵심 내용인것처럼
- 선형대수학에선 행렬이 핵심이다.
- Chapter 2에서 행렬에 대해 자세히 알아보는 시간을 가질 것이다.
1. Matrix Notation
- 행렬에 대해 나타내길 우리는 지금까지 다음과 같이 나타냈었다.
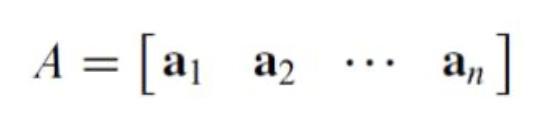
- 이를 조금 수정해 줄건데 기존의 행렬을 다음과 같이 i,j를 이용해여 인덱스를 설정해준 행렬을 확인해 보자.

- 우리는 앞으로 행렬A를 나타낼때 다음과 같이 나타낼 수 있다.

- 여기서 aij 의 의미는 행렬A에서 i번째 행, j번째 열에 해당하는 원소 를 뜻한다.
2. 항등행렬(Identity Matrix)
- 항등행렬(Identity Matrix)란 대각원소들의 값이 1이고 나머지값들은 0인 정방행렬을 의미한다.
ex)

3. Sums and Scalar Multiples
- 행렬은 벡터처럼 더할 수 있고, 스칼라를 곱해줄 수 있다.

ex)

3.1. 성질
- 각 행렬은 열 벡터(column vector)들로 이루어져있기 때문에 vector의 성질을 그대로 만족한다.
ex)

4. 행렬 곱(Matrix Multiplication)

- 이를 예제와 함께 보면 다음과 같다.
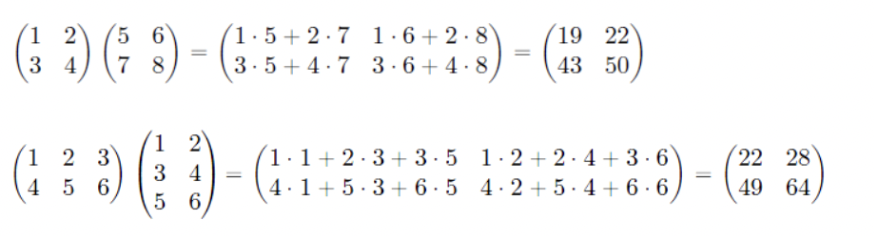
- m x n 행렬과 n x l행렬의 곱은 m x l 행렬이 된다.
4.1. 행렬곱의 성질
- 행렬곱은 다음과 같은 성질을 갖는다.

- 간단하게 요약하면 행렬곱은 결합법칙이 성립된다.
- 단 주의할 점은 교환법칙은 성립하지 않는다.
- 주의할 점.
1. AB != BA
2. AB = AC 라고 해서 B = C가 같다고 할수 없다.
3. AB = 0 라고 해서 A = 0 or B = 0 이라고 할 수 없다.
5. The Transpose of a Matrix

-즉,A의 행과 열을 뒤집어 주는 거라고 생각하면 편하다.
- 대각선을 기준으로 뒤집는다고 생각하면 된다.
ex)
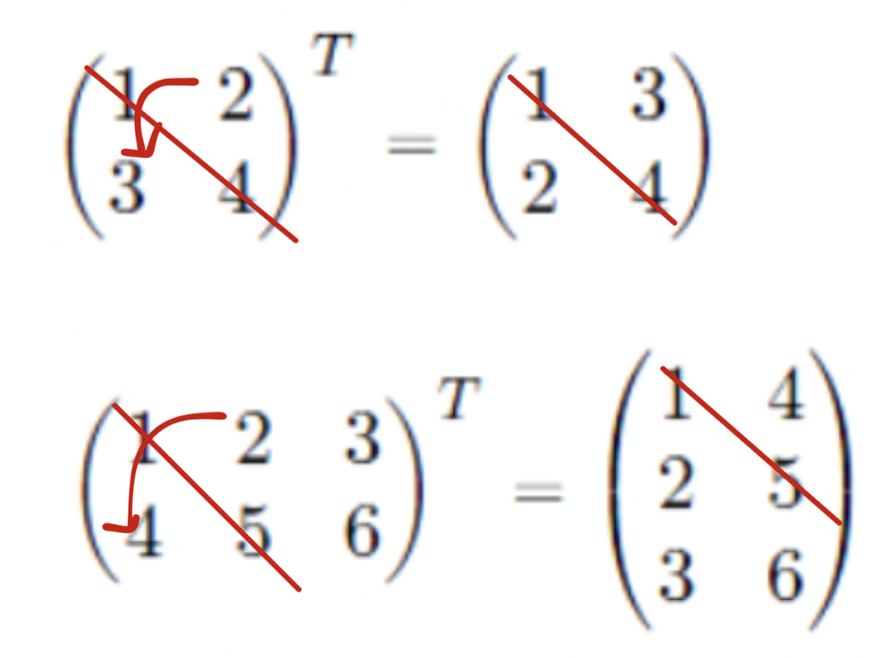
5.1.성질
- Transpose의 성질은 다음과 같다. (d의 내용은 까먹지 말아야 하는 중요한 성질이다.)

'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (5) | 2024.06.03 |
|---|---|
| [Linear Algebra] [2-2] The Inverse of a matrix (0) | 2024.06.03 |
| [Linear Algebra] [1-9] The Matrix of a Linear Transformation (0) | 2024.06.03 |
| [Linear Algebra] [1-8] Introduction to Linear Transformations (3) | 2024.06.03 |
| [Linear Algebra] [1-7] Linear Independence (0) | 2024.06.02 |

