0. Review
- 2-1 에선 행렬끼리 연산하는 방법에 대해서 알아보았다.
- 이번 챕터에선 역행렬에 대해서 알아보자.
1. 역행렬(Invertible matrix)
- n x n 정방행렬 A가 다음과 같은 조건을 만족할 때 역행렬이 존재(Invertible)한다라고 한다.

- 이때 A의 역행렬(Invertible Matrix)는 C가 된다.
또한 어떤 행렬의 역행렬(Invertible Matrix)는 오직 하나(unique)이다
proof)

- 이때 C를 A에 대한 기호로 나타내면 다음과 같다.

2. 역행렬 공식
- 2 x 2 행렬과 3 x 3 행렬의 역행렬을 구할 때 공식이 존재한다.
- 해당 포스트 에선 2 x 2 역행렬 공식만 다루도록 하겠다.
2.1. 2 x 2 역행렬 공식
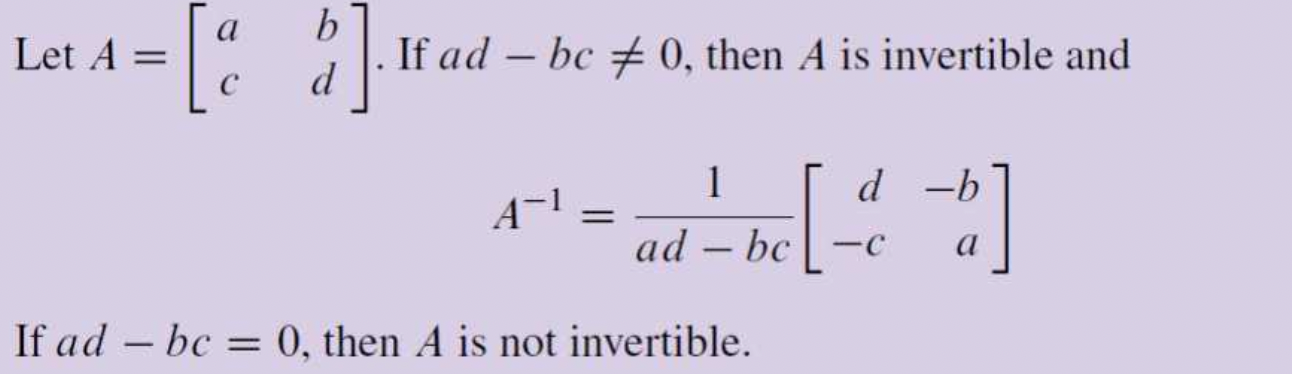
- 해당 역행렬 공식은 간단하기 때문에 암기를 해두는게 좋고
- 해당 역행렬 공식은 간단하게 가우스-조던 소거법(Gauss-jordan elimination)을 이용하여 쉽게 증명이 가능하다.
- 증명은 생략하겠다.
- 역행렬 공식에서 분모에 있는 ad-bc에 집중해보자.
- 만약 ad-bc = 0 이라면 해당 행렬 A는 역행렬을 가지지 않는다.
- 그래서 ad-bc는 해당 행렬이 invertible 한지 판별이 가능하다.
- 그래서 이를 식으로 나타내면 다음과 같다.

- determinant에 대한 자세한 내용은 챕터3에서 다루도록 할테니 식만 암기해두도록 하자.
3. 역행렬을 이용해서 해(Solution)찾기.
- 만약 A가 invertible 한 행렬이고 다음과 같은 식을 만족한다고 가정해보자
- Ax = b --> (A^-1)A x = A^-1 b --> Ix = A^-1 b --> x = A^-1 b
- x는 다음을 만족한다.

- 이를 이용하여 간단한 문제를 해결하자.
Q)

- 이를 Matrix Equation으로 나타내보자.


- A의 역행렬을 구해보자.

- 아래의 Matrix Equation의 양변에 A의 역행렬을 곱하면 다음과 같이 Solution을 구할 수 있다.

4. 역행렬의 성질
- 다음과 같은 성질을 보인다.
a.

b.
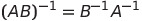
c.

5. 기본 행렬(Elementary matrix)
- 항등행렬 I에 딱 한번 row operation을 적용한 행렬을 기본 행렬(Elementary Matrix)라고 한다.
ex)

- E1 : replace row 3 by row3 -4row1
- E2 : Interchange row1 and row 2
- E3 : Scale row 3 by 5
- 만약 E1,E2,E3를 A라는 행렬에 곱하면 어떻게 될까?


- 보면 알겠지만, Elementary matrix를 곱해준다는 것은 행렬A에 해당하는 row operation을 해주는 것과 같다.
6. 가우스-조던 소거법(Gauss-jordan elimination)
[A I] 라는 강화행렬(Augmentrd matrix)를 row operation을 통해 [I A^(-1)] 로 만들어 내는 역행렬을 구하는 방법이다.
- 해당 방법이 성립하는 이유는 elementary matrix의 역행렬은 그 row operation의 역산과 같다 라는 성질로 성립이 가능하다.
ex)

'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-4] Partitioned Matrices (2) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (5) | 2024.06.03 |
| [Linear Algebra] [2-1] Matrix Operations (0) | 2024.06.03 |
| [Linear Algebra] [1-9] The Matrix of a Linear Transformation (0) | 2024.06.03 |
| [Linear Algebra] [1-8] Introduction to Linear Transformations (3) | 2024.06.03 |
0. Review
- 2-1 에선 행렬끼리 연산하는 방법에 대해서 알아보았다.
- 이번 챕터에선 역행렬에 대해서 알아보자.
1. 역행렬(Invertible matrix)
- n x n 정방행렬 A가 다음과 같은 조건을 만족할 때 역행렬이 존재(Invertible)한다라고 한다.

- 이때 A의 역행렬(Invertible Matrix)는 C가 된다.
또한 어떤 행렬의 역행렬(Invertible Matrix)는 오직 하나(unique)이다
proof)

- 이때 C를 A에 대한 기호로 나타내면 다음과 같다.

2. 역행렬 공식
- 2 x 2 행렬과 3 x 3 행렬의 역행렬을 구할 때 공식이 존재한다.
- 해당 포스트 에선 2 x 2 역행렬 공식만 다루도록 하겠다.
2.1. 2 x 2 역행렬 공식
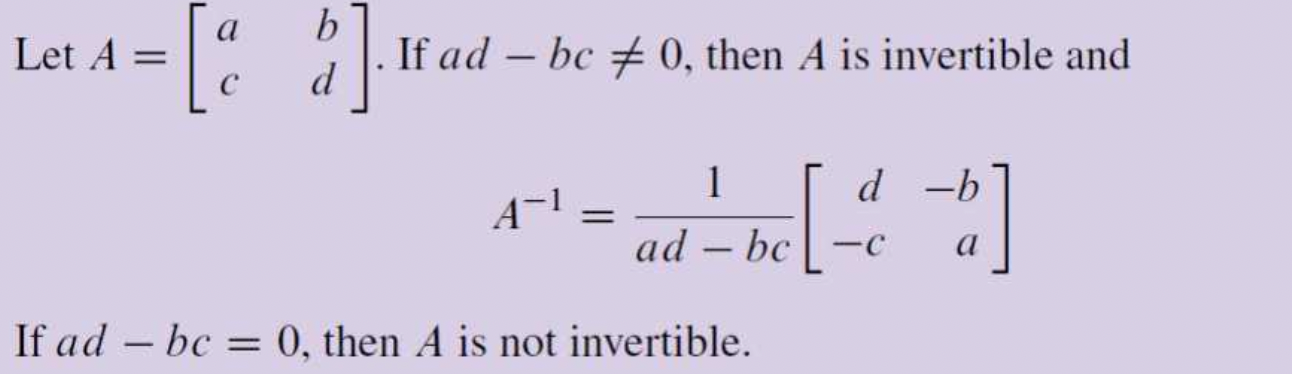
- 해당 역행렬 공식은 간단하기 때문에 암기를 해두는게 좋고
- 해당 역행렬 공식은 간단하게 가우스-조던 소거법(Gauss-jordan elimination)을 이용하여 쉽게 증명이 가능하다.
- 증명은 생략하겠다.
- 역행렬 공식에서 분모에 있는 ad-bc에 집중해보자.
- 만약 ad-bc = 0 이라면 해당 행렬 A는 역행렬을 가지지 않는다.
- 그래서 ad-bc는 해당 행렬이 invertible 한지 판별이 가능하다.
- 그래서 이를 식으로 나타내면 다음과 같다.

- determinant에 대한 자세한 내용은 챕터3에서 다루도록 할테니 식만 암기해두도록 하자.
3. 역행렬을 이용해서 해(Solution)찾기.
- 만약 A가 invertible 한 행렬이고 다음과 같은 식을 만족한다고 가정해보자
- Ax = b --> (A^-1)A x = A^-1 b --> Ix = A^-1 b --> x = A^-1 b
- x는 다음을 만족한다.

- 이를 이용하여 간단한 문제를 해결하자.
Q)

- 이를 Matrix Equation으로 나타내보자.


- A의 역행렬을 구해보자.

- 아래의 Matrix Equation의 양변에 A의 역행렬을 곱하면 다음과 같이 Solution을 구할 수 있다.

4. 역행렬의 성질
- 다음과 같은 성질을 보인다.
a.

b.
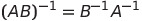
c.

5. 기본 행렬(Elementary matrix)
- 항등행렬 I에 딱 한번 row operation을 적용한 행렬을 기본 행렬(Elementary Matrix)라고 한다.
ex)

- E1 : replace row 3 by row3 -4row1
- E2 : Interchange row1 and row 2
- E3 : Scale row 3 by 5
- 만약 E1,E2,E3를 A라는 행렬에 곱하면 어떻게 될까?


- 보면 알겠지만, Elementary matrix를 곱해준다는 것은 행렬A에 해당하는 row operation을 해주는 것과 같다.
6. 가우스-조던 소거법(Gauss-jordan elimination)
[A I] 라는 강화행렬(Augmentrd matrix)를 row operation을 통해 [I A^(-1)] 로 만들어 내는 역행렬을 구하는 방법이다.
- 해당 방법이 성립하는 이유는 elementary matrix의 역행렬은 그 row operation의 역산과 같다 라는 성질로 성립이 가능하다.
ex)

'Mathematics Study > Linear Algebra (선형대수학)' 카테고리의 다른 글
| [Linear Algebra] [2-4] Partitioned Matrices (2) | 2024.06.04 |
|---|---|
| [Linear Algebra] [2-3] Characterizations of Invertible Matrices (5) | 2024.06.03 |
| [Linear Algebra] [2-1] Matrix Operations (0) | 2024.06.03 |
| [Linear Algebra] [1-9] The Matrix of a Linear Transformation (0) | 2024.06.03 |
| [Linear Algebra] [1-8] Introduction to Linear Transformations (3) | 2024.06.03 |

