0. Introduction
이번 섹션의 키워드는 두 개다.
- Mean Value Theorem (평균값 정리, MVT)
- l’Hôpital’s Rule (로피탈의 법칙)
둘 다 “**국소 정보(미분)**로부터 **전역 정보(평균 변화량, 극한, 비율)**를 읽는 방법”이라는 공통된 철학을 가진다.
- 평균값 정리:
- “구간 전체에서의 평균 기울기 = 어딘가 한 점에서의 순간 기울기”
즉,
$$\frac{f(b) - f(a)}{b - a} = f'(c) \quad\text{for some } c\in(a,b).$$ - 로피탈의 법칙:
- “$0/0$, $\infty/\infty$ 같은 애매한 비율의 극한은
각자 미분해서 생기는 비율의 극한으로 바꿔라”
즉,
$$\lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)}$$
(적절한 조건 하에서)
이번 포스팅에서는
- Rolle’s Theorem (로르의 정리)
- Mean Value Theorem (평균값 정리)와 직관 + 증명
- MVT 를 이용한 간단한 응용
- l’Hôpital’s Rule 의 아이디어와 공식
- 간단한 예제들
까지 정리해보자.
1. Rolle’s Theorem (의 정리)
평균값 정리는 바로 이 Rolle’s Theorem에서 출발한다.
정리 (Rolle’s Theorem)
연속함수 $f$ 가 다음을 만족한다고 하자.
- $f$ 가 $[a,b]$ 에서 연속이고, $(a,b)$ 에서 미분 가능
- $f(a) = f(b)$
그러면, 어딘가 한 점 $c\in(a,b)$ 에서
$$
f'(c) = 0
$$
이 되는 점이 존재한다.
쉽게 말하면,
양 끝 값이 같은 매끈한 그래프는
중간 어딘가에서 “기울기 0 (수평 접선)” 을 가진다.
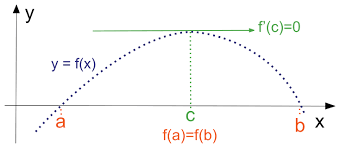
직관적인 이유
- $f$ 가 계속 이어져 있으면, $[a,b]$ 에서 최댓값 혹은 최솟값을 반드시 가진다. (Extreme Value Theorem)
- 그 최대/최소가 안쪽 $(a,b)$ 에서 나타난다면, 그 점에서 기울기는 0 이다.
- 만약 둘 다 끝점에서만 나타난다면?
- $f(a) = f(b)$ 이므로
- 최소는 안쪽 어딘가에서 나타날 수밖에 없다 → 그 점에서 $f'(c)=0$.
그래서 “양 끝 값이 같으면, 안쪽 어딘가에서 수평 접선이 있다”는 결론이 나온다.
2. Mean Value Theorem (평균값 정리)
이제 진짜 주인공인 평균값 정리(MVT).
정리 (Mean Value Theorem)
$f$ 가
- $[a,b]$ 에서 연속,
- $(a,b)$ 에서 미분 가능
이라고 하자.
그러면 어딘가 한 점 $c\in(a,b)$ 에서
$$
f'(c) = \frac{f(b) - f(a)}{b - a}
$$
가 되는 점이 존재한다.
즉,
구간 전체에서의 “평균 기울기”를
어딘가 한 점에서의 “순간 기울기”가 정확히 잡아준다.

2.1 MVT 증명 (Rolle’s Theorem 활용)
아이디어는 간단하다.
- 먼저 $[a,b]$ 를 잇는 직선을 생각한다:이 직선은
- $L(a) = f(a)$
- $L(b) = f(b)$
- $$
L(x) = f(a) + \frac{f(b) - f(a)}{b - a}(x - a)
$$ - 이제 새로운 함수를 생각하자. 그러면즉, $F(a) = F(b) = 0$ 이다.
- $$
F(a) = f(a) - L(a) = 0, \quad F(b) = f(b) - L(b) = 0
$$ - $$
F(x) = f(x) - L(x)
$$ - $f$ 와 $L$ 이 둘 다 $(a,b)$ 에서 미분 가능이므로
$F$ 역시 $(a,b)$ 에서 미분 가능, $[a,b]$ 에서 연속이다. - 따라서 Rolle’s Theorem 을 $F$ 에 적용할 수 있다.
$\Rightarrow$ 어떤 $c\in(a,b)$ 에 대해 - $$
F'(c) = 0
$$ - 그런데 $F'(x) = f'(x) - L'(x)$ 이므로,다시 쓰면
- $$
f'(c) = L'(c)
$$ - $$
0 = F'(c) = f'(c) - L'(c)
$$ - 그런데 $L'(x)$ 는 상수이고,따라서 모든 $x$ 에 대해 동일하다. 특히 $x=c$ 에서도가 된다. 증명 완료.
- $$
f'(c) = \frac{f(b) - f(a)}{b - a}
$$ - $$
L'(x) = \frac{f(b) - f(a)}{b - a}
$$
3. MVT 직관 & 간단한 예시
물리적 해석
- $f(t)$ 가 위치(position)라고 하고, $t$ 가 시간이라고 생각하자.
- 그럼 평균 속도는
- $$
\frac{f(b) - f(a)}{b - a}
$$ - 평균값 정리는 말한다:
- “그 구간 안 어딘가에서 실제 순간 속도 $f'(c)$ 가
정확히 평균 속도와 같은 순간이 존재한다.”
예제 1 — $f(x) = x^2$
$f(x) = x^2$ 를 $[1,3]$ 에서 보자.
- 평균 기울기:
- $$
\frac{f(3) - f(1)}{3 - 1}
= \frac{9 - 1}{2} = 4
$$ - 미분:따라서 $f'(c) = 4$ 가 되는 $c$ 는
- $$
2c = 4 \Rightarrow c = 2
$$ - $$
f'(x) = 2x
$$
즉,
$$
f'(2) = 4 = \frac{f(3) - f(1)}{3 - 1}
$$
MVT 가 보장하는 점 $c$ 는 이 경우 정확히 $2$ 가 된다.
예제 2 — $f(x) = \sin x$
$f(x) = \sin x$ 를 $[0,x]$ 에서 생각하면,
- 평균 기울기:
- $$
\frac{\sin x - \sin 0}{x - 0} = \frac{\sin x}{x}
$$ - $f'(t) = \cos t$
MVT에 따르면, $0$ 과 $x$ 사이 어딘가 $c$ 에 대해
$$
\cos c = \frac{\sin x}{x}
$$
즉,
$$
\sin x = (\cos c),x
$$
이 된다.
$x$ 가 작으면 $\cos c \approx 1$ 이므로,
$$
\sin x \approx x
$$
라는 익숙한 근사가 나온다. (여기서는 “정확히는 $\cos c$ 배”라는 정보를 더 갖고 있는 셈)
4. l’Hôpital’s Rule — 0/0, ∞/∞ 꼴 다루기
이제 두 번째 주인공, l’Hôpital’s Rule.
우리가 알고 싶은 건 이런 꼴이다:
$$
\lim_{x\to a}\frac{f(x)}{g(x)}
$$
그런데
- $f(x)\to 0$, $g(x)\to 0$ 이면 $\frac{0}{0}$ 꼴
- $f(x)\to \infty$, $g(x)\to \infty$ 이면 $\frac{\infty}{\infty}$ 꼴
둘 다 “불정형(indeterminate form)” 이라서
그냥 단순 대입으로는 아무 정보도 주지 않는다.
예를 들어,
- $\displaystyle \frac{x^2}{x}$ at $x\to 0$: $\frac{0}{0}$ 이지만 실제로는 $x$ → 0
- $\displaystyle \frac{\sin x}{x}$ at $x\to 0$: $\frac{0}{0}$ 이지만 실제로는 1
- $\displaystyle \frac{1 - \cos x}{x^2}$ at $x\to 0$: $\frac{0}{0}$ 이지만 실제 값은 $\frac{1}{2}$
즉,
“두 함수가 동시에 0(또는 ∞) 로 가는 속도”의 비율이 문제다.
4.1 로피탈의 법칙 (0/0 꼴)
조건은 대략 이렇다:
- $f$ 와 $g$ 는 $a$ 를 포함하는 어떤 열린 구간에서 미분 가능,
- $f(a) = g(a) = 0$,
- $g'(x) \neq 0$ (적어도 $a$ 근처에서),
- 그리고 $\displaystyle \lim_{x\to a} \frac{f'(x)}{g'(x)}$ 가 존재한다면,
결론:
$$\lim_{x\to a} \frac{f(x)}{g(x)}=\lim_{x\to a} \frac{f'(x)}{g'(x)}$$
(우변의 극한이 존재하고 유한하다고 가정)
아이디어만 간단히 보면:
- $f(a) = g(a) = 0$ 이므로, $f(x), g(x)$ 둘 다 $a$ 근처에서 0 으로 달려간다.
- 평균값 정리를 이용하면\frac{f'(c_1)}{g'(c_2)}
$$ - 꼴의 관계를 적당히 만들 수 있고, 여기서 $c_1, c_2$ 는 $x$ 와 $a$ 사이 어딘가.
- $$
\frac{f(x) - f(a)}{g(x) - g(a)} - $x\to a$ 로 보내면, $c_1, c_2$ 도 $a$ 근처로 끌려오고,
결과적으로 $\frac{f(x)}{g(x)}$ 의 극한이 $\frac{f'(x)}{g'(x)}$ 의 극한으로 이어진다.
(정확한 증명은 MVT 변형을 두 번 쓰는 구조인데, 여기서는 아이디어만)
5. l’Hôpital’s Rule 예제들
예제 1 — $\displaystyle \lim_{x\to 0} \frac{\sin x}{x}$
직접 쓰면 $\frac{0}{0}$ 꼴.
로피탈을 적용해보면,
- $f(x) = \sin x$, $f'(x) = \cos x$
- $g(x) = x$, $g'(x) = 1$
$$\lim_{x\to 0} \frac{\sin x}{x}=\lim_{x\to 0} \frac{\cos x}{1}\cos 0 = 1$$
예제 2 — $\displaystyle \lim_{x\to 0} \frac{1 - \cos x}{x^2}$
역시 $\frac{0}{0}$ 꼴.
- $f(x) = 1 - \cos x$, $f'(x) = \sin x$
- $g(x) = x^2$, $g'(x) = 2x$
한 번 미분하면
$$\lim_{x\to 0}\frac{1 - \cos x}{x^2}=\lim_{x\to 0}\frac{\sin x}{2x}$$
여전히 $\frac{0}{0}$ 꼴이므로 한 번 더 로피탈:
- $\sin x \mapsto \cos x$
- $2x \mapsto 2$
$$\lim_{x\to 0}\frac{\sin x}{2x}=\lim_{x\to 0}\frac{\cos x}{2}\frac{1}{2}$$
따라서
$$\lim_{x\to 0} \frac{1 - \cos x}{x^2} = \frac{1}{2}$$
예제 3 — $\displaystyle \lim_{x\to \infty} \frac{\ln x}{x}$
이번엔 $\frac{\infty}{\infty}$ 꼴이다.
- $f(x) = \ln x$, $f'(x) = \frac{1}{x}$
- $g(x) = x$, $g'(x) = 1$
로피탈 적용:
$$\lim_{x\to \infty} \frac{\ln x}{x}=\lim_{x\to \infty} \frac{1/x}{1}=\lim_{x\to \infty} \frac{1}{x} = 0$$
즉, $\ln x$ 도 무한대로 가지만, $x$ 에 비하면 훨씬 느리게 자라므로
비율은 0 으로 간다.
'Mathematics Study > Calculus (미적분학)' 카테고리의 다른 글
| [Calculus] [3-2] Antiderivatives (1) | 2025.11.21 |
|---|---|
| [Calculus] [3-1] The Idea of the Integral (0) | 2025.11.21 |
| [Calculus] [2-6] Newton’s Method (and Chaos) (0) | 2025.11.21 |
| [Calculus] [2-5] Parabolas, Ellipses, and Hyperbolas (0) | 2025.11.21 |
| [Calculus] [2-4] Graphs (0) | 2025.11.21 |