0. Introduction
이번 섹션은 지수함수 $b^x$ 와 로그함수 $\log_b y$ 의 기본 원리를 한눈에 정리하는 부분이다.
Strang 교수는 이 섹션을 “지수–로그의 전반적 구조를 먼저 잡는 챕터”라고 설명하며, 특히 $b^{m+n} = b^m b^n$ 이라는 단 하나의 원리가 모든 지수/로그 규칙의 출발점임을 강조한다.
또한 지수함수와 로그함수가 어떻게 서로 역(inverse) 관계인지를 그래프 수준에서 직관적으로 설명하고,
일반 좌표계(ordinary axes), 반로그(semi-log), 로그-로그(log-log) 그래프에서 어떤 함수가 직선이 되는지를 보여준다.
앞으로 나오는 미적분 계산(미분·적분)을 이해하기 위한 “지수/로그의 핵심 구조”를 다지는 섹션이라고 보면 된다.
1. 지수함수와 로그의 기본 원리
1.1 기본 예: 10의 거듭제곱
십진법에서 익숙한 숫자들:
- $10^0 = 1$
- $10^1 = 10$
- $10^2 = 100$
- $10^3 = 1000$
이때 로그(logarithm) 는 단순히 “지수를 꺼내는 연산”이다.
$$\log_{10} 1 = 0,\quad \log_{10} 10 = 1,\quad \log_{10} 100 = 2,\quad \log_{10} 1000 = 3.$$
즉 로그는 ‘그 숫자를 만들기 위해 필요한 지수’를 출력하는 함수이다.
음수 지수도 동일하게 적용된다
$10^{-1}$ 은 $1/10$,
$10^{-2}$ 은 $1/100$ 이므로
$$\log_{10}(1/10) = -1,\qquad \log_{10}(1/100) = -2.$$
1.2 지수법칙이 로그법칙을 만든다
가장 중요한 지수 규칙:
$$b^m b^n = b^{m+n}.$$
이것을 로그 관점으로 바꾸면 곱셈이 덧셈이 된다:
$$\log_b (yz) = \log_b y + \log_b z.$$
또 나눗셈은 지수의 차이이므로:
$$\log_b(y/z) = \log_b y - \log_b z.$$
이 단순한 성질 하나가 “로그가 계산을 쉽게 만드는 이유(곱셈을 덧셈으로 바꿈)”의 근본이다.
2. 밑(base)을 바꾸는 법: Change of Base
밑을 $b$ 에서 $a$ 로 바꾸고 싶을 때, 다음 규칙이 핵심이다:
$$b = a^{\log_a b}.$$
양변을 $x$ 제곱하면:
$$b^x = a^{(\log_a b), x}.$$
따라서 로그도 다음 규칙을 가진다.
$$\log_a y = (\log_a b), (\log_b y).$$
이는 (지수에서처럼) 밑을 바꿀 때 지수에 ‘배율’을 곱하면 된다는 뜻이다.
3. 지수함수와 로그함수의 그래프
지수함수 $y=b^x$ 와 로그함수 $x=\log_b y$ 는 서로 역함수이므로
그래프를 $y=x$ 선에 대해 대칭시키면 서로가 된다.
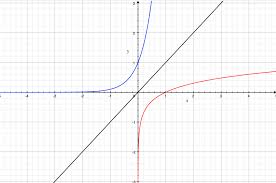
기본 성질:
- $b^x > 0$ 이므로 지수함수 그래프는 항상 x축 위에 있다.
- $\log_b y$ 는 $y>0$ 에서만 정의되므로, 그래프는 y축 왼쪽으로 절대 가지 않는다.
- 모든 지수함수는 $b^0=1$ 에서 시작한다.
3.1 일반 좌표계에서의 문제점
$2^x$, $4^x$ 같은 함수는 매우 빠르게 증가한다.
그래프는 빠르게 "수직처럼" 솟아올라 기본 성질을 읽기 어려워진다.
그래서 Strang은 로그 스케일(log scale) 을 사용해 더 정돈된 그래프를 볼 수 있도록 한다.
4. 로그 스케일을 이용한 그래프
4.1 Semi-log (x는 선형, y는 로그)
세미로그 그래프에서는 다음 사실이 놀랍게 단순해진다:
지수함수 $y = A b^x$ 가 직선이 된다
로그를 취하면:
$$\log y = \log A + x \log b.$$
즉 기울기 $\log b$ 를 가진 완벽한 직선이다.
기울기 = 로그의 밑의 로그값($\log b$) 이므로, 그래프의 기울기를 측정해 $b$ 값을 추정할 수 있다.
4.2 Log-log (두 축 모두 로그)
이번엔 거듭제곱(power) 함수를 생각해보자:
$$y = A x^k.$$
로그를 취하면:
$$\log y = \log A + k \log x.$$
이것도 직선이 된다.
여기서 기울기는 바로 “지수 $k$”.
따라서 log-log 그래프는 데이터가 거듭제곱 법칙을 따르는지 확인할 때 사용한다.
5. 지수함수의 미분: 아직은 c만 알고 넘어간다
지수함수를 미분할 때 핵심 식은 다음이다:
$$\frac{d}{dx} b^x = c, b^x.$$
여기서 $c$ 는 밑 $b$ 에 따라 달라지는 상수이다.
어디까지나 이 섹션에서는 “$b^x$ 의 미분이 자기 자신과 비례한다”는 구조만 이해한다.
이 $c$ 를 정확히 계산하는 것은 다음 섹션(6.2)에서 e를 정의할 때 해결된다.
그래서 지금은 단지:
- 지수함수는 기울기가 함수 자체에 비례하는 형태를 가진다.
- 이 사실 때문에 지수함수가 자연스럽게 성장/감소 모델에 등장한다.
Strang 교수는 이 구조를 ‘자연 법칙의 기본 틀’이라고 강조한다.
5.1 로그함수의 미분
지수함수의 역함수라는 사실을 이용하면:
$$\frac{dx}{dy} = \frac{1}{c,y}, \quad x = \log_b y.$$
즉
$$\frac{d}{dy} \log_b y = \frac{1}{c y}.$$
역시 상수 $c$ 가 등장한다.
결정적으로, 밑을 $b=e$ 로 선택하면 $c=1$ 이 된다는 것이 다음 섹션의 핵심이다.
'Mathematics Study > Calculus (미적분학)' 카테고리의 다른 글
| [Calculus] [4-3] Logarithms (0) | 2025.11.22 |
|---|---|
| [Calculus] [4-2] The Exponential $e^x$ (0) | 2025.11.22 |
| [Calculus] [3-5] The meaning and significance of definite integrals (0) | 2025.11.22 |
| [Calculus] [3-4] Indefinite Integrals and Substitutions (0) | 2025.11.21 |
| [Calculus] [3-3] Summation versus Integration (1) | 2025.11.21 |